応用情報技術者試験 過去問 2025年(令和7年) 春期 午後 問3
スライドパズルを解くプログラム
表1のルールで定義されるスライドパズルについて考える。
| 用語 | 説明 |
|---|---|
| 盤面 | 正方形の面に、1 から順に 1 ずつ大きくなる数字の書かれた駒が配置されている。1 か所だけ駒の置かれていない空白のマス(以下、空白マスという)がある。 |
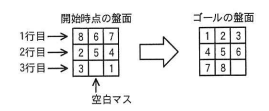
| 開始時点の盤面 ゴールの盤面 |
開始時点では、駒と空白マスはランダムに配置されている。 盤面左上に数字が 1 の駒があり、右の駒の数字は 1 ずつ増えていき、その行の右端の駒に書かれた数字より 1 大きい数字が、次の行の左端の駒の数字となる。盤面右下のマスが空白マスとなる。 |
| 駒の移動 | 駒の上下左右のいずれかに空白マスがある場合、駒を空白マスに移動することができる。駒が移動した場合、駒が置かれていたマスが空白マスになる。駒を空白マスに移動させて盤面を変化させ、ゴールの盤面と同じにすることを目指す。 |
一辺が3マスのスライドパズルの例を図1に示す。
本問では、一辺のマスの個数が任意のスライドパズルにおいて、ゴールの盤面になるまでの駒の移動回数が最小となる移動方法(以下、最小解という)を一つ求めるプログラムを作成する。
一辺がNマスのスライドパズルの最小解を幅優先探索を用いて求める方法
幅優先探索を行ったときの、スライドパズルの盤面の遷移を、グラフで表現する。開始時点の盤面をルートノード、ある時点の盤面をノード、駒の移動に伴う盤面の遷移をエッジで表現する。また、ゴールの盤面をゴールノードとして定義する。
幅優先探索で最小解を求める方法を次のように考える。ここで、Nは2以上とする。探索対象のノードに対して、移動できる駒ごとにその駒を移動した後のノードを作成して、探索対象のノードの子ノードとし、探索対象のノードは探索済みとなる。このとき、子ノードが表す盤面が既に探索したノード(以下、探索済みノードという)と同じであれば、この子ノードは終端ノードとして、以降の探索は行わない。また、子ノードがゴールノードと同じであれば、最小解が見つかったと判断して探索を終了する。
N が 3 の場合の例
一辺が3マスのスライドパズルの最小解を求める過程の例を図2に示す。
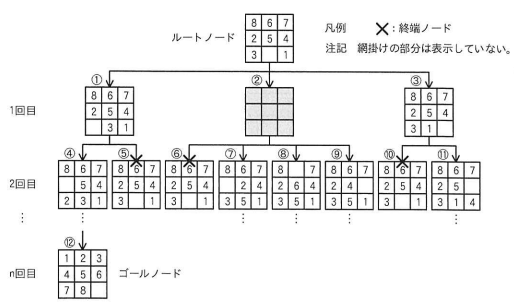
- 1回目の駒の移動では、ルートノードを探索対象のノードとする。ここでは、移動できる駒が三つあるので、ルートノードから深さが1となる①~③の子ノードを作成し、ルートノードは探索済みノードとなる。ここで、①~③の子ノードに対して、ゴールノードの判定及び終端ノードの判定を行う。
- 次に、作成した子ノードで終端ノード以外のノードをそれぞれ探索対象のノードとし、駒の移動にあわせて子ノードを作成する。図2では、①~③のノードから④~⑪の子ノードを作成し、①~③は探索済みノードとなる。ここで、④~⑪の子ノードに対して、ゴールノードの判定及び終端ノードの判定を行う。図2では、盤面が探索済みノードと一致する⑤、⑥及び⑪は終端ノードとなり、以降の探索は行わない。
- 以降、(2)で作成したノードの子ノードの作成と、ゴールノードの判定及び終端ノードの判定を繰り返す。図2の⑫は、n回目の移動でゴールノードに至ったことを示している。なお、全てのリーフノードが終端ノードと判定された場合、ゴールの盤面に至る駒の移動方法がないことを意味しているので、その旨のメッセージを出力して探索を終了する。
次に、配列を用いた盤面の表現方法を図3に示す。ここで、空白マスを表す値は最も大きい駒の数字である8に1を加えた9とする。なお、配列の要素番号は1から始まるものとする。

一辺がNマスのスライドパズルの最小解を求めるプログラム
一辺がNマスのスライドパズルにおいて、開始時点の盤面をランダムに作成し、最小解を求め、開始時点の盤面からの遷移及び駒の移動回数を出力するプログラムを作成する。開始時点からの盤面の遷移を保持する単方向連結リストの要素となるクラスBoardStateの説明を図4に、キューを表現するクラスQueueの説明を図5に、リストを表現するクラスListの説明を図6に、プログラムで使用する主な関数を表2に、最小解を求めるプログラムを図7に示す。
| メンバ変数 | 型 | 説明 |
|---|---|---|
| board | 整数型配列の配列 | 盤面配列。初期状態は未定義。 |
| space | 整数型の配列 | 空白マスの初期位置を示す行番号と列番号の二つの要素から成る配列。初期状態は未定義。 |
| prev | BoardState | 駒が1回移動する前の BoardState のインスタンスへの参照。開始地点の盤面からの遷移を出力する際に用いる。初期状態は未定義。 |
| コンストラクタ | 説明 |
|---|---|
| BoardState() | インスタンスを初期化する。 |
| BoardState(BoardState: st) |
インスタンスを初期化し、メンバ変数に次の処理を行う。
|
| コンストラクタ | 説明 |
|---|---|
| Queue() | 可変長のキューを生成する。 |
| メソッド | 戻り値 | 説明 |
|---|---|---|
| add(BoardState: st) | なし | キューに BoardState のインスタンスへの参照 st を追加する。 |
| isEmpty() | 論理型 | キューが空の場合は true を返し、空でない場合は false を返す。 |
| poll() | BoardState | 先頭の BoardState のインスタンスへの参照を取り出して返す。 |
| peek() | BoardState | 先頭の BoardState のインスタンスへの参照を返す。 |
| コンストラクタ | 説明 |
|---|---|
| List() | 可変長のリストを生成する。 |
| メソッド | 戻り値 | 説明 |
|---|---|---|
| add(整数型配列の配列: b) | なし | リストに盤面配列 b を追加する。 |
| isEmpty() | 論理型 | リストが空の場合は true を返し、空でない場合は false を返す。 |
| peek() | 整数型配列の配列 | リストの先頭に存在する盤面配列を返す。 |
| 名称 | 戻り値 | 説明 |
|---|---|---|
| createGoal(整数型: board_size) | 整数型配列の配列 | 引数board_sizeの値を一辺のマス数としたスライドパズルのゴールの盤面を表す配列(以下、ゴールの盤面配列という)を作成して返す。 |
| createStart(整数型: board_size) | 整数型配列の配列 | 引数board_sizeの値を一辺のマス数としたスライドパズルの開始時点の盤面配列をランダムに作成し、出力して返す。なお、ゴールの盤面配列と同じものが作成されることはない。 |
| getSpace(整数型配列の配列: b) | 整数型の配列 | 盤面配列bを参照して、空白マスの場所を行番号と列番号から成る配列で返す。 |
| checkGoal(整数型配列の配列: b, 整数型配列の配列: g) | 論理型 | 第一引数の盤面配列bと第二引数のゴールの盤面配列gを用いて両者が一致しているかどうかを判定して結果を返す。一致する場合はtrueを返し、一致しない場合はfalseを返す。 |
| printResult(BoardState: st) | なし | 引数として与えられたBoardStateのインスタンスへの参照stを用いて、開始時点の盤面からの遷移及び駒の移動回数を出力する。 |
| checkSameBoard(整数型配列の配列: b, List: l) | 論理型 | 引数で渡される探索済みの盤面配列のリストへの参照lを用いて、盤面配列bが探索済みの盤面配列のリストに存在するかどうかを判定して結果を返す。存在する場合はtrueを返し、存在しない場合はfalseを返す。 |
1: QSolveNPuzzle(整数型: board_size)
2: BoardState: start_state /* 開始時点の盤面を保持するBoardStateのインスタンス
への参照 */
3: 整数型配列の配列: goal_board /* ゴールの盤面配列 */
4: 整数型配列の配列: direction /* 駒の移動に伴う空白マスの移動方向を行番号の増減を番目
の要素、列番号の増減を番目の要素で表現する配列 */
5: Queue: explore_queue /* 探索対象の盤面を保持するキューのインスタンスへの参照 */
6: List: check_list /* 探索済みの盤面配列を保持するリストのインスタンス
への参照 */
7: BoardState: state /* 駒が移動する前の盤面を保持するBoardStateの
インスタンスへの参照 */
8: BoardState: new_state /* 駒が移動した後の盤面を保持するBoardStateの
インスタンスへの参照 */
9: 整数型: change_num /* 移動する駒の数字 */
10: 整数型: i /* forループ内で使用するカウンタ変数 */
11: start_state ← BoardState()
12: goal_board ← createGoal(board_size)
13: start_state.board ← createStart(board_size)
14: start_state.space ← getSpace(start_state.board)
15: direction ← {{1, 0}, {0, -1}, {-1, 0}, {0, 1}}
16: explore_queue ← Queue()
17: explore_queue.add(start_state)
18: check_list ← List()
19: check_list.add(start_state.board)
20: while (アがfalseと等しい)
21: state ← explore_queue.イ
22: for (iを1からdirectionの要素数まで1ずつ増やす)
23: if ((state.space[1] + ウが1以上) かつ
24: (state.space[1] + ウがエ以下) かつ
25: (state.space[2] + オが1以上) かつ
26: (state.space[2] + オがエ以下))
27: new_state ← BoardState(state)
28: new_state.space[1] ← state.space[1] + ウ
29: new_state.space[2] ← state.space[2] + オ
30: change_num ← new_state.board[new_state.space[1]][new_state.space[2]]
31: new_state.board[new_state.space[1]][new_state.space[2]] ← board_size × board_size
32: new_state.board[state.space[1]][state.space[2]] ← change_num
33: if (カがtrueと等しい)
34: printResult(new_state)
35: return
36: endif
37: if (checkSameBoard(new_state.board, check_list)がfalseと等しい)
38: explore_queue.キ
39: check_list.ク
40: endif
41: endif
42: endfor
43: endwhile
44: ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力
45: return