応用情報技術者試験 過去問 2019年(令和元年) 秋期 午後 問3
ニューラルネットワーク
AI技術の進歩によって、機械学習に利用されるニューラルネットワークは様々な分野で応用されるようになってきた。ニューラルネットワークが得意とする問題に分類問題がある。例えば、ニューラルネットワークによって手書きの数字を分類(認識)することができる。
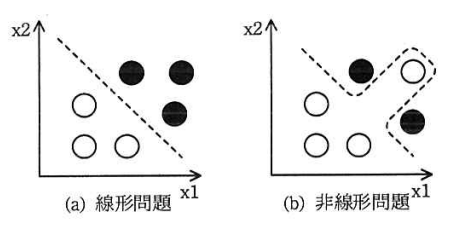
分類問題には線形問題と非線形問題がある。図1に線形問題と非線形問題の例を示す。2次元平面上に分布した白丸(○)と黒丸(●)について、線形問題(図1の(a))では1本の直線で分類できるが、非線形問題(図1の(b))では1本の直線では分類できない。機械学習において分類問題を解く機構を分類器と呼ぶ。ニューラルネットワークを使うと、線形問題と非線形問題の両方を解く分類器を構成できる。
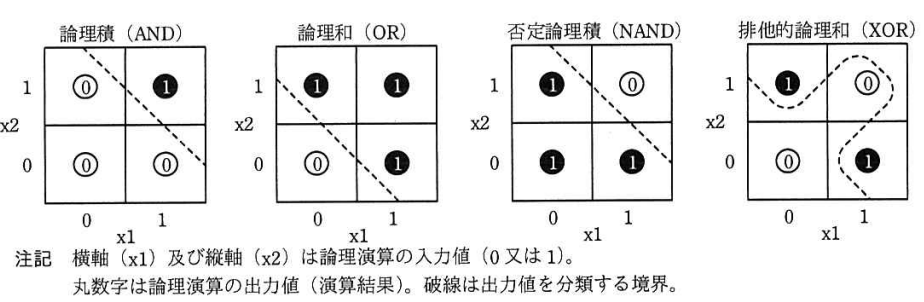
2入力の論理演算を分類器によって解いた例を図2に示す。図2の論理演算の結果(丸数字)は、論理積(AND)、論理和(OR)及び否定論理積(NAND)では1本の直線で分類できるが、排他的論理和(XOR)では1本の直線では分類できない。この性質から、前者は線形問題、後者は非線形問題と考えることができる。
単純パーセプトロンを用いた論理演算
ここでは、図2に示した四つの論理演算の中から、排他的論理和以外の三つの論理演算を、ニューラルネットワークの一種であるパーセプトロンを用いて、分類問題として解くことを考える。図3に最もシンプルな単純パーセプトロンの模式図とノードの演算式を示す。ここでは、円をノード、矢印をアークと呼ぶ。ノードx1及びノードx2は論理演算の入力値、ノードyは出力値(演算結果)を表す。ノードyの出力値は、アークがもつ重み(w1, w2)とノードyのバイアス(b)を使って、図3中の演算式を用いて計算する。
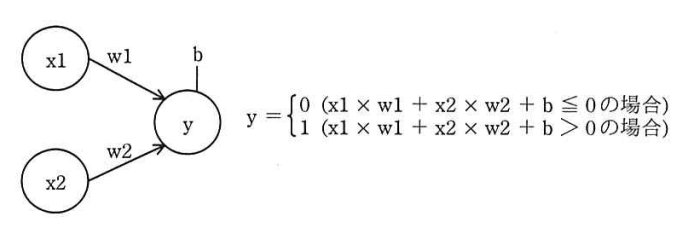
単純パーセプトロンに適切な重みとバイアスを設定することで、論理積、論理和及び否定論理積を含む線形問題を計算する分類器を構成することができる。一般に、重みとバイアスは様々な値を取り得る。表1に単純パーセプトロンで各論理演算を計算するための重みとバイアスの例を示す。
例えば、表1の論理和の重みとバイアスを設定した単純パーセプトロンにx1=1, x2=0を入力すると、図3の演算式から1×0.5+0×0.5−0.2=0.3>0となり、出力値はy=1となる。
| 論理演算 | w1 | w2 | b |
|---|---|---|---|
| 論理積 | 0.5 | 0.5 | a |
| 論理和 | 0.5 | 0.5 | −0.2 |
| 否定論理積 | −0.5 | −0.5 | 0.7 |
単純パーセプトロンのプログラム
単純パーセプトロンの機能を実装するプログラム simple_perceptron を作成する。
プログラムで使用する定数、変数及び配列を表2に、プログラムを図4に示す。simple_perceptron は、論理演算の入力値の全ての組合せXから論理演算の出力値Yを計算する。ここで、関数に配列を引数として渡すときの方式は参照渡しである。また、配列の添え字は0から始まるものとする。
| 名称 | 種類 | 説明 |
|---|---|---|
| NI | 定数 | 入力ノードの数を表す定数。 表1の論理演算では、2入力なので、2となる。 |
| NC | 定数 | 論理演算の入力値の全ての組合せの数を表す定数。 表1の論理演算では、4となる。 |
| X | 配列 | 論理演算の入力値の全ての組合せを表す2次元配列。 表1の論理演算では、[[0,0], [0,1], [1,0], [1,1]]が設定されている。 |
| Y | 配列 | 論理演算の出力値(演算結果)を格納する1次元配列。 表1の論理和では、入力値Xに対応して[0, 1, 1, 1]となる。 |
| WY | 配列 | ノードyのアークがもつ重みの値を表す1次元配列。 表1の論理和では、[0.5, 0.5]を与える。 |
| BY | 変数 | ノードyのバイアスの値(b)を表す変数。 表1の論理和では、−0.2を与える。 |
function simple_perceptron(X, Y)
for( out を 0 から NC−1 まで 1 ずつ増やす )
ytemp ← ア
for( in を 0 から NI−1 まで 1 ずつ増やす )
ytemp ← ytemp + イ × ウ
endfor
if( ytemp が エ )
Y[out] ← 1
else
Y[out] ← 0
endif
endfor
endfunction
3層パーセプトロンを用いた論理演算
パーセプトロンの層を増やすと、単純パーセプトロンでは解くことのできない非線形問題を解くことができるようになる。例えば排他的論理和を計算する分類器は、3層パーセプトロンを用いて構成することができる。
3層パーセプトロンの模式図とノードの演算式を図5に、排他的論理和を計算するための重みとバイアスの例を表3に示す。ノードm1及びノードm2を中間ノードと呼ぶ。
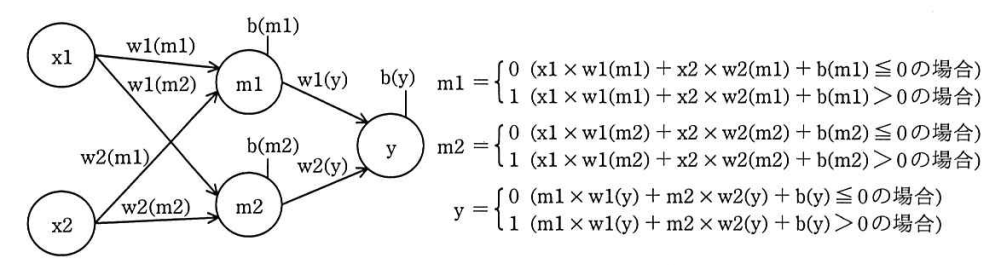
| ノード | w1 | w2 | b |
|---|---|---|---|
| m1 | 0.5 | 0.5 | −0.2 |
| m2 | −0.5 | −0.5 | 0.7 |
| y | 0.5 | 0.5 | −0.6 |
3層パーセプトロンのプログラム
3層パーセプトロンの機能を実装するプログラム three_layer_perceptron を作成する。表2に示したものに加えて、このプログラムで使用する定数及び配列を表4に、プログラムを図6に示す。three_layer_perceptron は、論理演算の入力値の全ての組合せXから論理演算の出力値Yを計算する。
| 名称 | 種類 | 説明 |
|---|---|---|
| NM | 定数 | 中間ノードの数を表す定数。 図5では、中間ノードがm1及びm2の二つなので、2となる。 |
| M | 配列 | 中間ノードの演算結果を格納する2次元配列。 |
| WM | 配列 | 中間ノードのアークがもつ重みの値を表す2次元配列。 表3の排他的論理和では、[[0.5, 0.5], [−0.5, −0.5]] を与える。 |
| BM | 配列 | 中間ノードのバイアスの値(b)を入れる1次元配列。 表3の排他的論理和では、[−0.2, 0.7] を与える。 |
function three_layer_perceptron(X, Y)
for( out を 0 から NC−1 まで 1 ずつ増やす )
ytemp ← ア
for( mid を 0 から NM−1 まで 1 ずつ増やす )
mtemp ← BM[mid]
for( in を 0 から NI−1 まで 1 ずつ増やす )
mtemp ← mtemp + イ × オ
endfor
if( mtemp が エ )
M[out][mid] ← 1
else
M[out][mid] ← 0
endif
ytemp ← ytemp + カ × キ
endfor
if( ytemp が エ )
Y[out] ← 1
else
Y[out] ← 0
endif
endfor
endfunction