2017年 春期 応用情報技術者試験 問3

探索アルゴリズム

1個ずつの重さが異なる商品を組み合わせ，合計の重さが指定された値になるようにしたい。

この問題を次のように簡略化し，解法を考える。

問題
指定されたn個の異なる数（自然数）の中から任意の個数の数を選択し，それらの合計が指定された目標Xに最も近くなる数の組合せを1組選択する。その際，合計はXよりも大きくても小さくてもよい。ただし，同じ数は1回しか選択できないものとする。

例えば，指定されたn個の数が（10，34，55，77），目標Xが100とすると，選択した数の組合せは（10，34，55），選択した数の合計（以下，合計という）は99となる。

この問題を解くためのアルゴリズムを考える。

指定されたn個の数の中から任意の個数を選択することから，各数に対して，選択する，選択しない，の二つのケースがある。数を一つずつ調べて，次の数がなくなるまで"選択する"，"選択しない"の分岐を繰り返すことで，任意の個数を選択する全ての組合せを網羅できる。この場合分けを図1に示す。

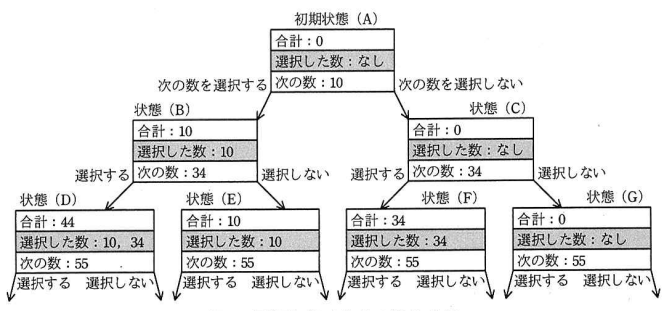
【データ構造の検討】

図1の場合分けをプログラムで実装するために，必要となるデータ構造を検討する。

まず，図1の場合分けを木構造とみなしたときの各ノード（状態）を構造体Statusで表す。構造体Statusは要素として"合計"，"選択した数"，"次の数"をもつ必要がある。

プログラムで使用する配列，変数及び構造体を表1に示す。

表1 プログラムで使用する配列，変数及び構造体
名称種類内容
numbers[]配列問題で指定されるn個の数を格納する配列。配列の添字は1から始まる。
target変数問題で指定される目標Xを格納する変数。
Status構造体次の三つの要素をもつ構造体。状態を表す。
・total：合計を表す数数。初期値は0。
・selectedNumbers[]：選択した数を表す配列。各要素の初期値はnullとする。配列の添字は1から始まる。
・nextIndex：次の数のnumbers[]における添字を格納する変数。初期値は1。
次の数がない場合は0。
構造体の要素は"."を使った表記で表す。"."の左に，構造体全体を表す変数を書き，"."の右に，要素名を書く。
currentStatus変数構造体Statusの値を格納する変数。"取得した状態"を表す。
ansStatus変数構造体Statusの値を格納する変数。"現時点での解答の候補"（以下，"解答の候補"という）を表す。初期値はnullとする。

【探索の手順】

図1に示した場合分けの初期状態（A）からの探索手順を，次の(1)～(3)に示す。

① これから探索する状態を格納しておくためのデータ構造として，キューを使用する場合とスタックを使用する場合で，探索の順序が異なる。また，② データ構造によってメモリの使用量も異なる。ここではキューを使用することにする。

② 初期状態（A）を作成し，キューに格納する。キューが空になるまで(2)，(3)を繰り返す。

③ キューに格納されている状態を一つ取り出す。これを"取得した状態"と呼ぶ。"取得した状態"の評価を行う（状態を評価する手順は次の["取得した状態"の評価]に示す）。

探索の手順

"取得した状態"に次の数がある場合，次の数を選択した状態と，次の数を選択しない状態をそれぞれ作成し，順にキューに格納する。

【"取得した状態"の評価】

"取得した状態"を評価し，"解答の候補"を設定する手順を，次の(1)，(2)に示す。

① "解答の候補"がnullの場合，"取得した状態"を"解答の候補"にする。

② "解答の候補"がnullでない場合，"解答の候補"の合計と"取得した状態"の合計をそれぞれ目標Xと比較して，後者の方が目標Xに近い場合，"取得した状態"を"解答の候補"にする。

"取得した状態"の評価

探索の手順が終了した時点の"解答の候補"を解答とする。

探索を行うための関数を表2に示す。

表2 探索を行うための関数
名称内容
enqueue(s)引数として与えられる構造体Statusの値sをキューに追加する。
dequeue()キューから構造体Statusの値を取り出して返す。
isEmpty()キューが空かどうかを判定する。
キューが空ならば1を，そうでなければ0を返す。
nextStatus1(s)引数として与えられる構造体Statusの値sに対して，次の数を選択した状態を表す構造体Statusの値を返す。戻り値の各要素に次の内容を設定する。
・total：s.total+numbers[s.nextIndex]を設定する。
・selectedNumbers[]：s.selectedNumbers[]にnumbers[s.nextIndex]を追加した配列を設定する。
・nextIndex：s.nextIndexが0ならば0を，そうでなければs.nextIndex+1を設定する。
nextStatus2(s)引数として与えられる構造体Statusの値sに対して，次の数を選択しない状態を表す構造体Statusの値を返す。戻り値の各要素に次の内容を設定する。
・total：s.totalを設定する。
・selectedNumbers[]：s.selectedNumbers[]を設定する。
・nextIndex：s.nextIndexが0ならば0を，そうでなければs.nextIndex+1を設定する。
abs(n)引数として与えられる数nの絶対値を返す。

【探索処理関数 treeSearch】

探索処理を実装した関数treeSearchのプログラムを図2に示す。

ここで，表1で定義した配列及び変数は，グローバル変数とする。

function treeSearch( )
  currentStatus を初期化する                     //初期状態を作成する
  enqueue( currentStatus )                      //初期状態をキューに格納する
  while(ア)
    currentStatus ← dequeue()                   //キューから状態を取り出す
    if( ansStatus が null である )
      イ
    elseif( abs(target-ansStatus.total)が abs(target-currentStatus.total)よりも大きい )
      ウ
    endif
    if(エ) <-- (α)
      enqueue( nextStatus1(currentStatus) )     //次の数を選択した状態をキューに追加する
      enqueue( nextStatus2(currentStatus) )     //次の数を選択しない状態をキューに追加する
    endif
  endwhile
endfunction
図2 関数treeSearchのプログラム

【探索回数の削減】

関数treeSearchで実装した方法では，nが大きくなるにつれて"取得した状態"を評価する回数（以下，探索回数という）も増大するが，不要な探索処理を行わないようにすることによって，③探索回数を削減することができる。探索回数の削減のために，探索を継続するかどうかを示すフラグを新たに用意し，次の(1)～(3)の処理を追加することにした。

① "取得した状態"の合計が目標X以上の場合，以降の状態で数を選択しても合計は目標Xから離れてしまい，"解答の候補"にはならない。以降の状態の探索を不要とするために，フラグを探索中止に設定する。

② (1)以外の場合，フラグを探索継続に設定する。

③ フラグが探索中止の場合，"取得した状態"からの分岐を探索しないようにする。

探索回数の削減のために追加する変数

探索回数の削減のために追加する変数を表3に示す。

表3 探索回数の削減のために追加する変数
名称種類内容
nextFlag変数"Y"のとき探索継続，"N"のとき探索中止を表す。

探索回数の削減を実装するために，図2中の（α）の行と（β）の行の間に図3のプログラムを追加し，（β）を"if（エ，かつ，nextFlagが"Y"である）"に修正した。

if( currentStatus.total が target 以上である )
  nextFlag ← オ
else
  nextFlag ← カ
endif
図3 探索回数の削減のための追加プログラム
平成29年度 春期 応用情報技術者試験 午後 問3