応用情報技術者試験 過去問 2016年(平成28年) 春期 午後 問3
ライフゲーム
ライフゲームとは,数学者コンウェイが考案した,生命の誕生,生存,死滅などを再現したシミュレーションゲームである。マス目状の盤上の各マスに生命が存在でき,そのマス自身及び隣接するマスの状態によって次世代の誕生,生存,死滅が決まる。その条件を表1に示す。
なお,隣接するマスには,斜め方向のマスも含む。また,生命が存在するマスを"生のマス",生命が存在しないマスを"死のマス"と呼ぶ。
| 条件名 | 条件 |
|---|---|
| 誕生 | 死のマスに隣接する生のマスが三つならば,死のマスは次の世代では生のマスとなる。 (死のマスに隣接する生のマスが三つ以下又は四つ以上ならば,死のマスは次の世代でも死のマスである。) |
| 生存 | 生のマスに隣接する生のマスが二つ又は三つならば,生のマスは次の世代でも生のマスである。 |
| 過疎 | 生のマスに隣接する生のマスが一つ以下ならば,生のマスは過疎によって次の世代では死のマスとなる。 |
| 過密 | 生のマスに隣接する生のマスが四つ以上ならば,生のマスは過密によって次の世代では死のマスとなる。 |
4×4マスのシミュレーション
4×4マスの盤上における第3世代までのシミュレーションを図1に示す。
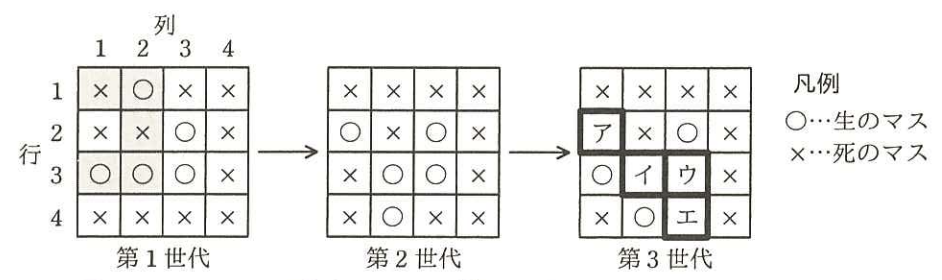
第1世代は,初期値として設定されたものである。例として,第1世代の2行目1列目のマスを考える。現在,このマスは死のマスである。このマスに隣接するマスを網掛けで示す。これら五つのマスの中に生のマスが三つある。これは表1の"誕生"の条件に該当するので,第2世代の2行目1列目のマスは生のマスになる。同様に,第1世代の各マスについて,そのマス自身及び隣接するマスの状態を確認することで第2世代が決まる。次の世代への状態の更新は,全てのマスについて同時に行われる。
盤上のマスのデータ構造
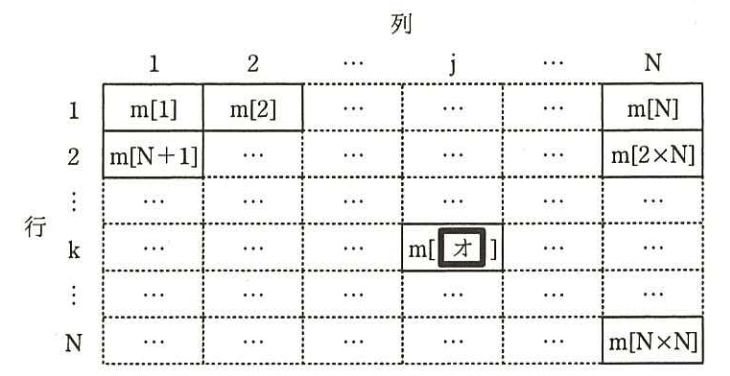
N×Nマスの盤上の状態を表現するデータ構造を考える。多次元配列が利用できないプログラム言語を考慮し,盤上の各マスの生死状態を管理するデータ構造として1次元配列mを用いる。配列mのデータ構造のイメージを図2に示す。
配列mを次世代に更新するプログラム
使用する定数,配列及び関数を表2に,配列mを次世代に更新する関数updateを図3に示す。
なお,関数に配列を引数として渡すときの方式は参照渡しである。
| 名称 | 種類 | 説明 |
|---|---|---|
| N | 定数 | 盤の一辺の大きさ。3以上の整数が入る。 |
| m | 配列 | N×Nマスの生死状態を管理する1次元配列。生の場合は1が,死の場合は0が入る。 |
| temp | 配列 | 配列mと同じ大きさの1次元配列。 |
| copy(array1, array2) | 関数 | 配列array1の全ての要素を配列array2にコピーする。 |
| clear(array) | 関数 | 配列arrayの全ての要素の値を0にする。 |
function update(m)
copy(m, temp) // 配列mを配列tempにコピーして退避する
clear(m) // 配列mの全ての要素の値を0にする
for( iを1からN×Nまで1ずつ増やす )
if( i-1がNで割り切れる ) ┐
a ← 0 │
b ← 1 │
elseif( iが1がNで割り切れる ) ├ α
a ← -1 │
b ← 0 │
else │
a ← -1 │
b ← 1 │
endif ┘
e ← 0
for( yを-1から1まで1ずつ増やす )
for( xをaからbまで1ずつ増やす )
if( (yと0が等しくない) or (xと0が等しくない) )
c ← i + y×N + x
if( (cが1以上) and (cがN×N以下) )
if( カ )
e ← e+1
endif
endif
endif
endfor
endfor
// 生死を判定する
if( キ )
m[i] ← 1
elseif( (temp[i]と1が等しい) and ((eと2が等しい) or (eと3が等しい)) )
ク
endif
endfor
endfunction
テストプログラム
図3のプログラムをテストするために,配列mに第1世代が与えられたときの第p世代が,机上で作成した正しい結果である配列rと等しいことを確認するプログラムを作成した。作成した関数shouldBeを図4に示す。ここで,pには2以上の整数が入る。
1: function shouldBe( m, p, r ) 2: for( iを1からpまで1ずつ増やす ) 3: update(m) 4: endfor 5: for( iを1からN×Nまで1ずつ増やす ) 6: if( m[i]とr[i]が等しくない ) 7: return false // テスト失敗 8: endif 9: endfor 10: return true // テスト成功 11: endfunction
図3のプログラムが正しく動作する状態で図4のプログラムを実行したところ,テストが失敗した。原因を調査した結果,図4のケ行目に問題があることが判明したので,①プログラムを修正してテストを成功させることができた。