2016年 秋期 応用情報技術者試験 問3

魔方陣

魔方陣とは，正方形のマス目（方陣）に数を配置し，縦・横・対角線のいずれにおいても，その並びの数の合計が同じになるものである。ここでは，N×Nの方陣（Nは3以上の自然数）に1からN²までの数を適不足なく配置したものとする。このとき，縦・横・対角線のN個のマスの合計値は，いずれも（ア + N）÷2となる。

Nが3の場合の魔方陣の一つを図1に示す。

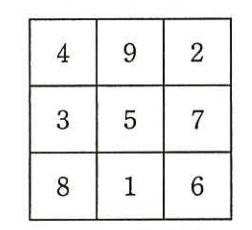
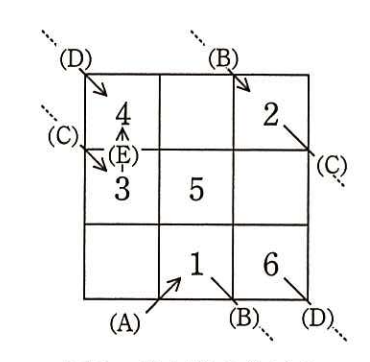
Nが奇数の場合，魔方陣の一つを次の手順で作ることができる。N=3のときに，この手順によって1～6の数が配置される様子を図2に示す。

【魔方陣の作り方】

魔方陣の作り方は，次のとおりである。ここで(A)～(E)は図2中の該当箇所を示す。

1. N×Nの全てのマスは何も入っていない空白の状態とする。
2. 最下行の中央のマスを現在位置とし，現在位置に数1を配置する(A)。
3. 現在位置の右下のマスが空白かどうか確認する。このとき，最下行の下は最上行(B)，最右列の右は最左列(C)とする。右下隣の右下は，左上隣(D)である。
4. (3)で確認したマスが空白の場合は，そこを新しい現在位置とする。(3)で確認したマスが空白でない場合は，現在位置の上のマスを新しい現在位置とする(E)。この際，新しい現在位置が最上行よりも上になることはない。
5. 数を一つ増やし，現在位置にその数を配置する。
6. 全てのマスが埋まるまで，(3)～(5)を繰り返す。

【魔方陣のプログラム】

魔方陣の数の配置を記憶する，整数型の2次元配列houjinを用意する。配列の添字は1から始まる。行y列xのマスは，houjin[y][x]で表現する。例えば，図1中の1が配置されているマスは，houjin[3][2]である。

数の配置に関する判定をするために，配列houjinの領域を(N+1)×(N+1)の大きさで用意し，適切な初期値を設定する。Nが3の場合の例を図3に示す。数が既に配置されているかどうかを判定するために，図3の太枠内の各マスの初期値は0とする。

また，現在位置の右下のマスが太枠の外であることを判定するために，4行目のマスにSOTO_SHITA，4列目のマスにSOTO_MIGI，行4列4のマスにSOTO_KADOの三つの異なる定数（0からN²までの整数以外の整数）を初期値として設定する。

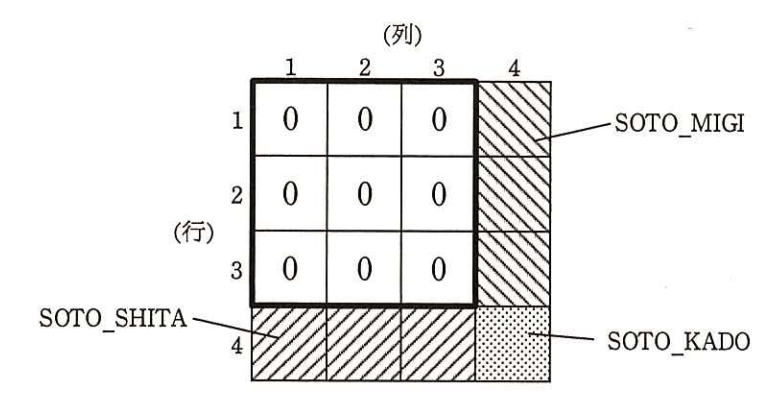
配列houjinの初期化をする関数shokika，及び数を配置する関数mahoujinのプログラムを図4に示す。引数Nは，正の奇数（N≧3）である。

function shokika(N)
    for( y を1からNまで1ずつ増やす )
        for( x を1からNまで1ずつ増やす )
            houjin[y][x] ← 0
        endfor
        イ ← SOTO_MIGI
    endfor
    for( x を1からNまで1ずつ増やす )
        ウ ← SOTO_SHITA
    endfor
    houjin[N+1][N+1] ← SOTO_KADO
endfunction

function mahoujin(N)
    y ← N
    エ
    suuji ← 1
    houjin[y][x] ← suuji
    
    while( suuji が オ )
        yb ← y
        xb ← x
        
        y ← y+1
        x ← x+1
        if( houjin[y][x]がSOTO_SHITAと等しい )
            y ← 1
        elseif( houjin[y][x]がSOTO_MIGIと等しい )
            x ← 1
        elseif( houjin[y][x]がSOTO_KADOと等しい )
            y ← 1
            x ← 1
        endif
        
        if( houjin[y][x]が0と等しくない )
            y ← カ
            x ← キ
        endif
        
        suuji ← suuji+1
        houjin[y][x] ← suuji
        
    endwhile
endfunction

【プログラムの判定部分の改変】

図4のプログラムによるメモリ使用量の削減のために，配列houjinの領域をN×Nに縮小し，定数SOTO_SHITA，SOTO_MIGI及びSOTO_KADOを使わないようにするプログラムの改変を考えた。図4の(F)の部分を改変したプログラムを図5に示す。

y ← y+1
x ← x+1
if( y が ク よりも大きい )
    y ← ケ
endif
if( x が ク よりも大きい )
    x ← ケ
endif