応用情報技術者試験 過去問 2015年(平成27年) 秋期 午後 問3
2分探索木
2分探索木とは、全てのノードNに対して、次の条件が成立している2分木のことである。
- Nの左部分木にある全てのノードのキー値は、Nのキー値よりも小さい。
- Nの右部分木にある全てのノードのキー値は、Nのキー値よりも大きい。
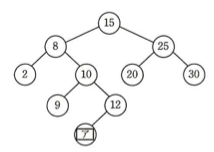
ここで、ノードのキー値は自然数で重複しないものとする。2分探索木の例を図1に示す。図中の数はキー値を表している。
2分探索木を実現するために、ノードを表す構造体Nodeを定義する。構造体Nodeの構成要素を表1に示す。
| 構成要素 | 説明 |
|---|---|
| key | キー値 |
| left | 左子ノードへの参照 |
| right | 右子ノードへの参照 |
構造体の実体を生成するためには、次のように書く。
new Node(key)
生成した構造体への参照が戻り値となる。構造体の構成要素のうち、keyは引数keyの値で初期化され、leftとrightはnullで初期化される。
変数pが参照するノードをノードpという。ノードを参照する変数からそのノードの構成要素へのアクセスには"."を用いる。例えば、ノードpのキー値には、p.keyでアクセスできる。
なお、変数pの値がnullの場合、木は空である。
[2分探索木でのノードの探索]
与えられたキー値をもつノードを探索する場合、親から子の方向へ、木を順次たどりながら探索を行う。
探索する2分探索木にノードがない場合は、目的のノードが見つからず、探索は失敗と判断して終了する。探索する2分探索木にノードがある場合は、与えられたキー値と木の根のキー値を比較し、等しければ、目的のノードが見つかったので探索は成功と判断して終了する。与えられたキー値の方が小さければ左部分木に、大きければ右部分木に移動する。移動先の部分木でも同様に探索を続ける。
この手順によって探索を行う関数searchのプログラムを図2に示す。このプログラムでは、探索が成功した場合は見つかったノードへの参照を返し、失敗した場合はnullを返す。
//ノードpを根とする2分探索木から、キー値がkであるノードを探索する
function search(k, p)
if(p と null が等しい)
return null //探索失敗
elseif(k と p.key が等しい)
return p //探索成功
elseif(イ)
return search(k, p.left) //左部分木を探索する
else
return search(k, p.right) //右部分木を探索する
endif
endfunction
[2分探索木へのノードの挿入]
2分探索木にノードを挿入する場合、探索と同様に、親から子の方向へ、木を順次たどりながら、適切な位置にノードを挿入する。
挿入する2分探索木にノードがない場合は、挿入するキー値のノードを作成する。
挿入する2分探索木にノードがある場合は、挿入するキー値と木の根のキー値を比較し、挿入するキー値の方が小さければ左部分木に、大きければ右部分木に移動する。移動先の部分木でも同様の処理を続ける。
この手順によって挿入を行う関数addNodeのプログラムを図3に示す。このプログラムでは、挿入の結果として得られた2分探索木の根のノードへの参照を返す。ただし、このプログラムは、挿入するキー値と同じキー値をもつノードが2分探索木に既に存在するときは何もしない。
//ノードpを根とする2分探索木に、キー値がkであるノードを挿入する
function addNode(k, p)
if(p と null が等しい)
p ← ウ //ノードを生成する
elseif(k と p.key が等しくない)
if(イ)
p.left ← addNode(k, p.left) //左部分木に移動し挿入を続ける
else
p.right ← addNode(k, p.right) //右部分木に移動し挿入を続ける
endif
endif
エ
endfunction
[2分探索木からのノードの削除]
2分探索木から、あるキー値をもつノードを削除する場合、次の(1)~(3)の手順を行う。
- 2分探索木にノードがない場合は、何もしないで処理を終了する。
- 削除するキー値と木の根のキー値を比較し、削除するキー値の方が小さければ左部分木に、大きければ右部分木に移動する。移動先の部分木でも同様の処理を続ける。
- 削除するキー値と木の根のキー値が等しい場合、削除するキー値をもつノードを削除するため、次の(3-1)~(3-3)を実行する。
- 削除するノードが子ノードをもたない場合、そのノードを削除する。
- 削除するノードが子ノードを一つだけもつ場合、削除するノードの位置にその子ノードを置く。
- 削除するノードが左右両方に子ノードをもつ場合、削除するノードの左部分木の中で最大のキー値をもつノードを左部分木から取り除き、削除するノードの位置に置く。
この手順を使って2分探索木からノードの削除を行う関数removeNodeのプログラムを図4に示す。このプログラムでは、削除した後の2分探索木の根のノードへの参照を返す。ただし、このプログラムは、削除するキー値をもつノードが2分探索木に存在しないときは何もしない。
図4中の関数extractMaxNodeは、引数で指定されたノードを根とする2分探索木の中で最大のキー値をもつノードを木から削除し、削除されたノードへの参照を大域変数extractedNodeに設定した上で、削除した後の2分探索木の根のノードへの参照を返す。関数extractMaxNodeのプログラムを図5に示す。
//ノードpを根とする2分探索木から、キー値がkであるノードを削除する
function removeNode(k, p)
if(p と null が等しくない)
if(k が p.key より小さい)
p.left ← removeNode(k, p.left)
elseif(k が p.key より大きい)
p.right ← removeNode(k, p.right)
else
if(p.left と null が等しい かつ p.right と null が等しい)
p ← null //ノードを削除する
elseif(オ と null が等しい)
p ← p.right //右部分木を置く
elseif(カ と null が等しい)
p ← p.left //左部分木を置く
//左部分木の中の最大ノードを置く
else
p.left ← extractMaxNode(p.left)
r ← extractedNode
r.left ← p.left
r.right ← p.right
p ← キ
endif
endif
endif
return p
endfunction
//ノードpを根とする2分探索木から、最大のキー値をもつノードを削除し、削除された
//ノードへの参照を大域変数に格納する
function extractMaxNode(p)
if(p.right と null が等しい)
extractedNode ← p
p ← p.left
else
p.right ← extractMaxNode(p.right)
endif
return p
endfunction
[2分探索木の計算量]
2分探索木における計算量は、木の高さに依存する。図2の関数searchを使ってn個のノードから成る2分探索木を探索する場合、想定される最大の計算量は、O(ク)である。木構造が完全2分木であれば、その計算量は最大でもO(ケ)である。