2014年 春期 応用情報技術者試験 問3

循環小数の循環節を検出するアルゴリズム

与えられた自然数 n について，1/n の小数表現を考える。1/n は，割り切れない場合，必ず循環小数となる。本問において，循環小数は，図1に示すように，繰り返し現れる数の並びである循環節の先頭から末尾までを括弧でくくる表記法で表す。

1 を n で割る割り算で現れる余りは，1 から n-1 までの値に限られる。循環小数となる場合は，割り算を小数第 1 位から行っていくと，どこかでそれまでに現れた余りと同じ値の余りが現れる。以降の割り算で得られる小数は，同じ数の並びが繰り返されることとなり，その数の並びが循環節となる。循環節の桁数は最大 n-1 である。

1/56 の計算で商を 1 桁ずつ求めていくと，余りの遷移は図2 のようになる。ここでは，前のマスの中の値を 10 倍して 56 で割った余りが次のマスの中の値となる。余りとして 48 が再現されることから，1/56 では小数第 4 位から第 9 位までが循環節となることが分かる。

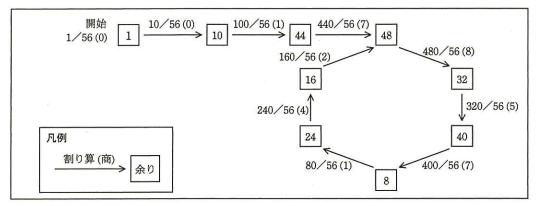
【循環節を検出するアルゴリズム】

単純に余りを配列に記録して，既出の余りであるかどうかを比較することによって循環節を検出する方法では，割り算の各行で現れる余りの種類の最大である n-1 種類の余りを記録する必要がある。その配列の大きさは n に比例することになり，処理できる n の値は使用可能な記憶域の大きさによって制約される。そこで記憶域の制約を受けない，"ウサギとカメ"に例えられるフロイドの循環検出法のアルゴリズムを用いる。

この検出法は，循環するデータの先頭と末尾の位置を効率よく検出できることが証明されている。

図2の余りを格納したマスから次のマスへ割り算を 1 行進めることを，"ウサギとカメ"の歩みに例えて 1 歩進むという。

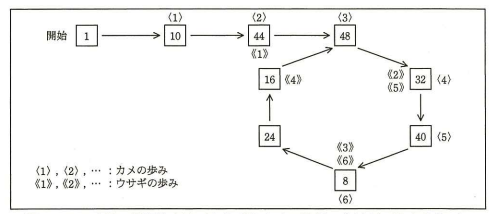
このアルゴリズムでは，まず，図3 に示すように，カメは (1)，(2)，... と一度に 1 歩ずつ，ウサギは (1)，(2)，... と一度に 2 歩ずつ進む。両者は同時に出発し，進んだマス（(1) と (1)，(2) と (2)，...）の余りを比較しながら，余りが一致するところ（(6) と (6)）まで進む。

このように，循環小数となる全ての n において，ウサギは循環部分の何巡目かで周回遅れのカメに必ず追い付き，両者の余りは一致する。

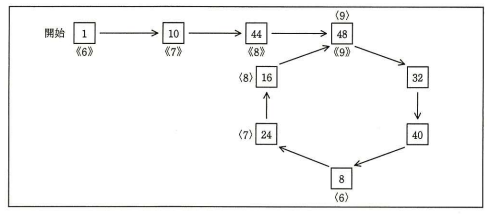
両者の余りが一致したら，図4 に示すように，カメは引き続き，ウサギは最初に戻って今度は両者とも 1 歩ずつ進む。最初に両者の余りが一致したところ（(9) と (9)）の次の割り算の商が，循環節の先頭である。

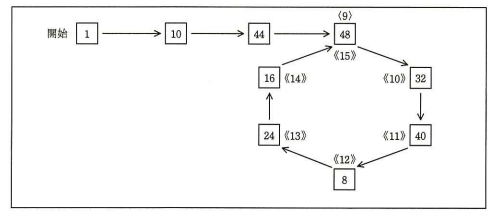
循環節の先頭を検出した後，図5 に示すように，ウサギだけが再びカメと余りが一致するところ（(9) と (15)）まで 1 歩ずつ進むことによって，循環節の末尾を検出する。

このアルゴリズムを使って循環節の先頭と末尾の桁位置を求める関数 junkan を図6 に示す。図6で使用する変数と関数は，表1のとおりである。

function junkan(n)
  m ← 1
  p ← 1
  s ← 0
  t ← 0
  while(true)
    m ← amari(m * 10, n)    // カメが1歩進む
    p ← amari(amari(p * 10, n) * 10, n)    // ウサギが2歩進む
    if(ア)
      break
    endif
  endwhile
  if(p が 0 と等しくない)
    イ
    s ← 1
    while(ウ)
      s ← s + 1
      m ← amari(m * 10, n)
      p ← amari(p * 10, n)
    endwhile
    p ← amari(p * 10, n)
    エ
    while(m が p と等しくない)
      t ← t + 1
      p ← amari(p * 10, n)
    endwhile
  endif
  return(s, t)
endfunction

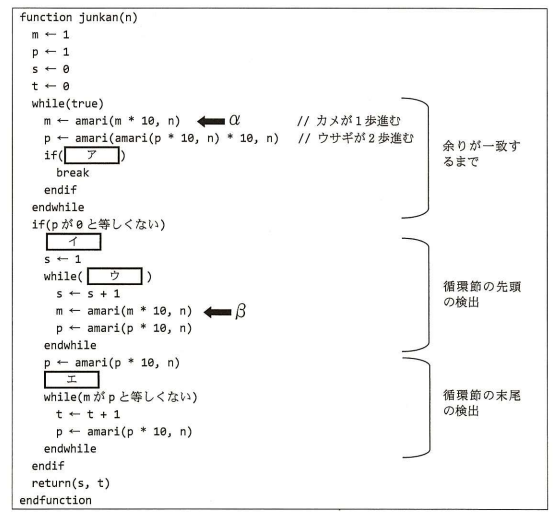
与えられた n に基づき，0 記法で表した場合，関数 junkan のプログラムが必要とする記憶域の大きさは オ となり，計算量は カ となる。