応用情報技術者試験 過去問 2013年(平成25年) 春期 午後 問2
一般的な表記法の数式を逆ポーランド表記法に変換するアルゴリズム
逆ポーランド表記法とは、演算子を二つの演算対象の後ろに配置することによって、数式を表現する表記法である。例えば、一般的な表記法の数式 1+2×3 を、逆ポーラ ンド表記法では 123×+ と表記する。
逆ポーランド表記法で表記した数式は、数値や演算子を左から順に処理すればよく、括弧を使う必要もないので、コンピュータが数式を取り扱うのに都合が良い。
一般的な表記法の数式から逆ポーランド表記法への変換は、スタックを用いること で容易に実現できる。
逆ポーランド表記法への変換アルゴリズム
一般的な表記法の数式を逆ポーランド表記法に変換するアルゴリズムでは、まず変換前の数式を、数値、演算子及び括弧の要素(以下、演算要素という)に分解する。
演算子には二項演算子+,-,×,÷を用い、括弧には "(" と ")" を用いる。
数値は0~9の1桁の数とする。それぞれの演算要素には、優先度を定義する。
変換の処理には、変換前配列、スタック及び変換後配列を用いる。初期状態では、変換前配列には変換前の数式の演算要素が順に入っており、スタックと変換後配列は空の状態である。変換後には、変換後配列に逆ポーランド表記法に変換した結果が入る。例えば、変換前の数式が1+2×3の場合、初期状態は表1のようになる。

逆ポーランド表記法への変換は、次の(1)~(4)の手順で行う。
- 変換前配列の先頭から順に、演算要素を1個参照する。参照する演算要素がない場合は手順4に進む。
- スタック上に演算要素がある場合は、スタックの先頭にある演算要素の優先度を参照し、手順1の演算要素の優先度以上なら、スタックの先頭の演算要素をポップし、変換後配列の末尾に追加する。これを、スタックの先頭の演算要素の優先度が、手順1の演算要素の優先度未満になるまで繰り返す。ただし、スタックの先頭の演算要素が "(" の場合は、そこで繰り返しを終了する。
- 手順1で参照した演算要素が ")" なら、それを破棄し、その際スタックの先頭にあるはずの "(" もポップして破棄した後手順1に戻る。手順1で参照した演算要素が ")" 以外なら、その演算要素をスタックにプッシュし、手順1に戻る。
- スタック上にある全ての演算要素を順番にポップし、変換後配列の末尾に追加する。
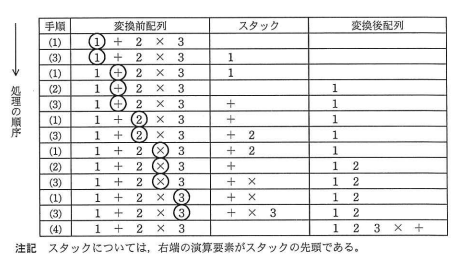
演算要素の優先度を表2に、数式1+2×3を変換するときの処理過程を図1に示す。
なお、図1中の丸で囲った演算要素は、(1)の手順で参照した演算要素である。
| 演算要素 | 優先度 |
|---|---|
| ( | 5 |
| 数値 | 4 |
| ア、イ | 3 |
| ウ、エ | 2 |
| ) | 1 |
逆ポーランド表記法への変換プログラム
逆ポーランド表記法への変換プログラムを作成した。プログラム中で使用する主な変数、配列及び関数を表3に、作成したプログラムを図2に示す。
図2のプログラムでは、スタックの取扱いを容易にするために、ダミーの演算要素nullを定義し、プログラム開始直後にスタックにプッシュしている。
nullがスタックからポップされることがないようにするために、その優先度をオと定義する。こうすることで、プログラム中、手順(2)の処理を行う部分でカの判定処理を記述する必要がなくなり、プログラムが簡潔になる。
| 種別 | 名称 | 型又は戻り値の型 | 説明 |
|---|---|---|---|
| 関数 | GetElement(index) | 演算要素 | 変換前配列のindex番目の演算要素を返す。indexが1の場合は先頭の演算要素を返す。 |
| 変数 | elementCount | 正の整数 | 変換前の数式に含まれる演算要素の個数。 |
| 関数 | GetPriority(element) | 非負の整数 | elementで指定された演算要素の優先度を表す非負の整数を返す。 |
| 配列 | result[] | 演算要素の配列 | 変換後配列。添字は1から始まる。配列の大きさは十分に大きいものとする。 |
| 変数 | resultCount | 非負の整数 | 変換後配列にある演算要素の個数。 |
| 配列 | stack[] | 演算要素の配列 | スタックとして使用する配列。添字は1から始まる。配列の大きさは十分に大きいものとする。 |
| 変数 | stackCount | 非負の整数 | スタックにある演算要素の個数。 |
resultCount ← 0
stackCount ← 1
stack[stackCount] ← null
i ← 1
while (i が elementCount 以下の間繰り返す)
elementPriority ← GetPriority(GetElement(i))
stackTop ← キ ← ①
// 演算要素をスタックからポップし、変換後配列の末尾に追加する。
while ( ク かつ stackTop が "(" 以外の間繰り返す)
resultCount ← resultCount + 1
result[resultCount] ← stackTop
stackCount ← stackCount - 1
stackTop ← キ
endwhile
// 変換前配列を参照し、演算要素を処理する。
if ( ケ )
stackCount ← stackCount - 1
else
stackCount ← stackCount + 1
stack[stackCount] ← GetElement(i)
endif
i ← i + 1
endwhile
// スタックに残った演算要素を、変換後配列の末尾に追加する。
while ( キ が null でない間繰り返す)
resultCount ← resultCount + 1
result[resultCount] ← キ
stackCount ← stackCount - 1
endwhile
エラーチェックの追加
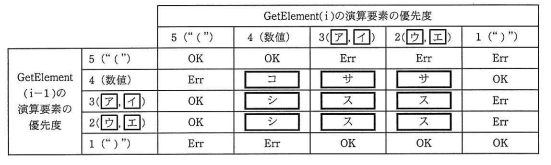
図2のプログラムの①の箇所において、iが2以上のとき、GetElement(i-1)の優先度と、GetElement(i)の優先度を比較することによって、簡易的な入力エラーチェックを追加することができる。例えば、数値の演算要素が2個以上連続する場合や、")" の直後に "(" が続く場合など、四則演算の式として不正なものがあった場合はエラーとする。
入力エラーとする条件を表4に示す。GetElement(i-1)の優先度と、GetElement(i)の優先度について、表4に従って評価をした結果、"OK"の場合は、そのまま処理を続行する。評価した結果が"Err"の場合は、入力された数式が誤っていると判断して処理を中断する。