応用情報技術者試験 過去問 2022年(令和4年) 秋期 午後 問3
迷路の探索処理
始点と終点を任意の場所に設定する n×m の 2 次元のマスの並びから成る迷路の解を求める問題を考える。本問の迷路では次の条件で解を見つける。
- 迷路内には障害物のマスがあり、n×m のマスを囲む外壁のマスがある。障害物と外壁のマスを通ることはできない。
- 任意のマスから、そのマスに隣接し、通ることのできるマスに移動できる。迷路の解とは、この移動の繰返しで始点から終点にたどり着くまでのマスの並びである。ただし、迷路の解では同じマスを 2 回以上通ることはできない。
- 始点と終点は異なるマスに設定されている。
5×5 の迷路の例を示す。解が一つの迷路の例を図 1 に、解が複数(四つ)ある迷路の例を図 2 に示す。
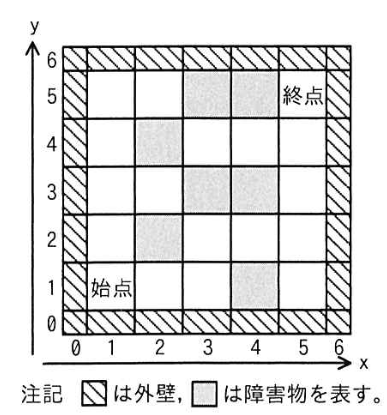
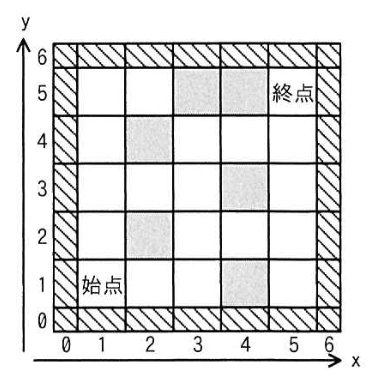
迷路の解を見つける探索
迷路の解を全て見つける探索の方法を次のように考える。
迷路と外壁の各マスの位置を x 座標と y 座標で表し、各マスについてそのマスに関する情報(以下、マス情報という)を考える。与えられた迷路に対して、障害物と外壁のマス情報には NG フラグを、それ以外のマス情報には OK フラグをそれぞれ設定する。マス情報全体を迷路図情報という。
探索する際の "移動" には、"進む" と "戻る" の二つの動作がある。"進む" は、現在いるマスから① y 座標を 1 増やす、② x 座標を 1 増やす、③ y 座標を 1 減らす、④ x 座標を 1 減らす、のいずれかの方向に動くことである。マスに "進む" と同時にそのマスのマス情報に足跡フラグを入れる。足跡フラグが入ったマスには "進む" ことはできない。"戻る" は、今いるマスから "進んで" きた一つ前のマスに動くことである。マスに "移動" したとき、移動先のマスを "訪問" したという。
探索は、始点のマスのマス情報に足跡フラグを入れ、始点のマスを "訪問" したマスとして、始点のマスから開始する。現在いるマスから次のマスに "進む" 試みを①~④の順に行い、もし試みた方向のマスに "進む" ことができないならば、次の方向に "進む" ことを試みる。4 方向いずれにも "進む" ことができないときには、現在いるマスのマス情報を OK フラグに戻し、一つ前のマスに "戻る"。これを終点に到達するまで繰り返す。終点に到達したとき、始点から終点まで "進む" ことでたどってきたマスの並びが迷路の解の一つとなる。
迷路の解を見つけた後も、他の解を見つけるために、終点から一つ前のマスに "戻り"、迷路の探索を続け、全ての探索を行ったら終了する。迷路を探索している間、それまでの経過をスタックに格納しておく。終点にたどり着いた時点でスタックの内容を順番にたどると、それが解の一つになる。
図 1 の迷路では、始点から始めて、(1,1)→(1,2)→(1,3)→(1,4)→(1,5)→(2,5)→(1,5)→(1,4)のように "移動" する。ここまででマスの "移動" は 7 回起きていて、このときスタックには経過を示す 4 個の座標が格納されている。さらに探索を続けて、始めから 13 回目の "移動" が終了した時点では、スタックには ア 個の座標が格納されている。
迷路の解を全て求めて表示するプログラム
迷路の解を全て求めて表示するプログラムを考える。プログラム中で使用する主な変数、定数及び配列を表 1 に示す。配列の添字は全て 0 から始まり、要素の初期値は全て 0 とする。迷路を探索してマスを "移動" する関数 visit のプログラムを図 3 に、メインプログラムを図 4 に示す。メインプログラム中の変数及び配列は大域変数とする。
| 名称 | 種類 | 内容 |
|---|---|---|
| maze[x][y] | 配列 | 迷路図情報を格納する 2 次元配列 |
| OK | 定数 | OK フラグ |
| NG | 定数 | NG フラグ |
| VISITED | 定数 | 足跡フラグ |
| start_x | 変数 | 始点の x 座標 |
| start_y | 変数 | 始点の y 座標 |
| goal_x | 変数 | 終点の x 座標 |
| goal_y | 変数 | 終点の y 座標 |
| stack_visit[k] | 配列 | それまでの経過を格納するスタック |
| stack_top | 変数 | スタックポインタ |
| sol_num | 変数 | 見つけた解の総数 |
| paths[u][v] | 配列 | 迷路の全ての解の座標を格納する 2 次元配列。添字の u は解の番号、添字の v は解を構成する座標の順番である。 |
function visit(x, y)
maze[x][y] ← VISITED //足跡フラグを入れる
stack_visit[stack_top] ← (x, y) //スタックに座標を入れる
if(x が goal_x と等しい かつ y が goal_y と等しい) //終点に到達
for(k を 0 から stack_top まで 1 ずつ増やす)
イ ← stack_visit[k]
endfor
sol_num ← sol_num+1
else
stack_top ← stack_top+1
if(maze[x][y+1]が OK と等しい)
visit(x, y+1)
endif
if(maze[x+1][y]が OK と等しい)
visit(x+1, y)
endif
if(maze[x][y-1]が OK と等しい)
visit(x, y-1)
endif
if(maze[x-1][y]が OK と等しい)
visit(x-1, y)
endif
stack_top ← ウ
endif
エ ← OK
endfunction
function main
stack_top ← 0
sol_num ← 0
maze[x][y]に迷路図情報を設定する
start_x, start_y, goal_x, goal_y に始点と終点の座標を設定する
visit(start_x, start_y)
if( オ が 0 と等しい)
"迷路の解は見つからなかった" と印字する
else
paths[][]を順に全て印字する
endif
endfunction
解が複数ある迷路
図 2 は解が複数ある迷路の例で、一つ目の解が見つかった後に、他の解を見つけるために、迷路の探索を続ける。一つ目の解が見つかった後で、最初に実行される関数 visit の引数の値は カ である。この引数の座標を基点として二つ目の解が見つかるまでに、マスの "移動" は キ 回起き、その間に座標が (4,2) のマスは ク 回 "訪問" される。