応用情報技術者試験 過去問 2021年(令和3年) 春期 午後 問3
クラスタ分析に用いるk-means法
k-means法によるクラスタ分析は、異なる性質のものが混ざり合った母集団から互いに似た性質をもつものを集め、クラスタと呼ばれる互いに素な部分集合に分類する手法である。新聞記事のビッグデータ検索、店舗の品ぞろえの分類、教師なし機械学習などで利用されている。ここでは、2次元データを扱うこととする。
分類方法と例
N個の点をK個(N未満)のクラスタに分類する方法を次に示す。
- N個の点(1からNまでの番号が付いている)からランダムにK個の点を選ぶ(以下、初期設定という)。それらの点をコアと呼ぶ。コアには1からKまでのコア番号を付ける。なお、K個のコアの座標は全て異なっていなければならない。
- N個の点とK個のコアとの距離をそれぞれ計算し、各点から見て、距離が最も短いコア(複数存在する場合は、番号が最も小さいコア)を選ぶ。選ばれたコアのコア番号を、各点が所属する1回目のクラスタ番号(1からK)とする。ここで、二つの点をXY座標を用いてP=(a, b)とQ=(c, d)とした場合、PとQの距離を√(a-c)²+(b-d)²で計算する。
- K個のクラスタのそれぞれについて、クラスタに含まれる全ての点を使って重心を求める。ここで、重心のX座標をクラスタに含まれる点のX座標の平均、Y座標をクラスタに含まれる点のY座標の平均と定義する。ここで求めた重心の番号はクラスタの番号と同じとする。
- N個の点と各クラスタの重心(G₁, ⋯, Gₖ)との距離をそれぞれ計算し、各点から見て距離が最も短い重心(複数存在する場合は、番号が最も小さい重心)を選ぶ。選ばれた重心の番号を、各点が所属する次のクラスタ番号とする。
- 重心の座標が変わらなくなるまで、(3)と(4)を繰り返す。
次の座標で与えられる7個の点を、この分類方法に従い、二つのクラスタに分類する例を図1に示す。
P₁=(1,0) P₂=(2,1) P₃=(4,1) P₄=(1.5,2) P₅=(1,3) P₆=(2,3) P₇=(4,3)
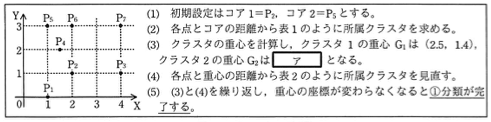
| 点 | コア1との距離 | コア2との距離 | 所属クラスタ番号 |
|---|---|---|---|
| P₁ | √2 | 3 | 1 |
| P₂ | 0 | √5 | 1 |
| P₃ | 2 | √13 | 1 |
| P₄ | √5/2 | √5/2 | 1 |
| P₅ | √5 | 0 | 2 |
| P₆ | 2 | 1 | 2 |
| P₇ | 2√2 | 3 | 1 |
| 点 | 重心G₁との距離 | 重心G₂との距離 | 次の所属クラスタ番号 |
|---|---|---|---|
| P₁ | 2.05 | 3.04 | 1 |
| P₂ | 0.64 | 2.06 | 1 |
| P₃ | 1.55 | 3.20 | 1 |
| P₄ | 1.16 | 1.00 | 2 |
| P₅ | 2.19 | 0.50 | 2 |
| P₆ | 1.67 | 0.50 | 2 |
| P₇ | 2.19 | 2.50 | 1 |
クラスタ分析のプログラム
この手法のプログラムを図2に、プログラムで使う主な変数、関数及び配列を表3に示す。ここで、配列の添字は全て1から始まり、要素の初期値は全て0とする。
| 名称 | 種類 | 内容 |
|---|---|---|
| core[t] | 配列 | コア番号がtである点P_mの番号mを格納する。 |
| initial(K) | 関数 | 初期設定として次の処理を行う。第s回目の点(P₁, P₂, ⋯, P_N)からランダムに異なるK個を抽出し、その番号を順に配列coreに格納する。 |
| data_dist(s, t) | 関数 | 点P_sとコア番号がtである点の距離を返す。 |
| grav_dist(s, t) | 関数 | 点P_sと重心G_tの距離を返す。 |
| data_length[t] | 配列 | ある点から見た、コア番号がtである点との距離を格納する。 |
| grav_length[t] | 配列 | ある点から見た、重心G_tとの距離を格納する。 |
| min_index() 引数は data_length 又は grav_length |
関数 | 配列の中で、最小値が格納されている添字sを返す。最小値が二つ以上ある場合は、最も小さい添字を返す。 例 右の配列に対する戻り値は2 添字 1 2 3 4 5 配列 5 1 4 1 3 |
| cluster[s] | 配列 | 点P_sが所属するクラスタ番号を格納する。 |
| coordinate_x[s] | 配列 | 重心G_sのX座標を格納する。 |
| coordinate_y[s] | 配列 | 重心G_sのY座標を格納する。 |
| gravity_x(s) | 関数 | クラスタsの重心G_sを求め、そのX座標を返す。 |
| gravity_y(s) | 関数 | クラスタsの重心G_sを求め、そのY座標を返す。 |
| flag | 変数 | フラグ(値は0又は1) |
function clustering (N, K) //Nはデータ数、Kはクラスタ数
MaxCount ← 100 //無限ループを防ぐため最大見直し回数を設定
initial(K) //初期設定
for( s を 1 から N まで 1 ずつ増やす ) //クラスタを決定(1回目)
for( t を 1 から K まで 1 ずつ増やす )
data_length[t] ← data_dist(s, core[t])
endfor
cluster[s] ← min_index(data_length)
endfor
for( p を 1 から MaxCount まで 1 ずつ増やす ) //クラスタを見直す
if( p が 1 と等しい )
for( イ ) //1回目の重心の計算
coordinate_x[t] ← gravity_x(t)
coordinate_y[t] ← gravity_y(t)
endfor
else
ウ
for( イ ) //2回目以降の重心の計算
if( gravity_x(t)と coordinate_x[t]が異なる //重心を修正する
又は gravity_y(t)と coordinate_y[t]が異なる )
coordinate_x[t] ← gravity_x(t)
coordinate_y[t] ← gravity_y(t)
flag ← 1
endif
endfor
if( エ ) //終了して抜ける
return
endif
endif
for( s を 1 から N まで 1 ずつ増やす ) //近い重心を見つける
for( t を 1 から K まで 1 ずつ増やす )
grav_length[t] ← grav_dist(s,t)
endfor
オ
endfor
endfor
endfunction
初期設定の改良
このアルゴリズムの最終結果は初期設定に依存し、そこでのコア間の距離が短いと適切な分類結果を得にくい。そこで、関数initialにおいて一つ目のコアはランダムに選び、それ以降はコア間の距離が長くなる点が選ばれやすくなるアルゴリズムを検討した。検討したアルゴリズムでは、t番目までのコアが決まった後、t+1番目のコアを残った点から選ぶときに、それまでに決まったコアから離れた点を、より高い確率で選ぶようにする。具体的には、それまでに決まったコア(コア1~コアt)と、残った N-t 個の点からPsとの距離の和をTsとする。N-t個の全ての点についてTsを合計し、Tsがカほど高い確率で点Psが選ばれるようにする。このとき、点Psがt+1番目のコアとして選ばれる確率としてキを適用する。