2018年 春期 応用情報技術者試験 問3

ナイトの巡歴問題

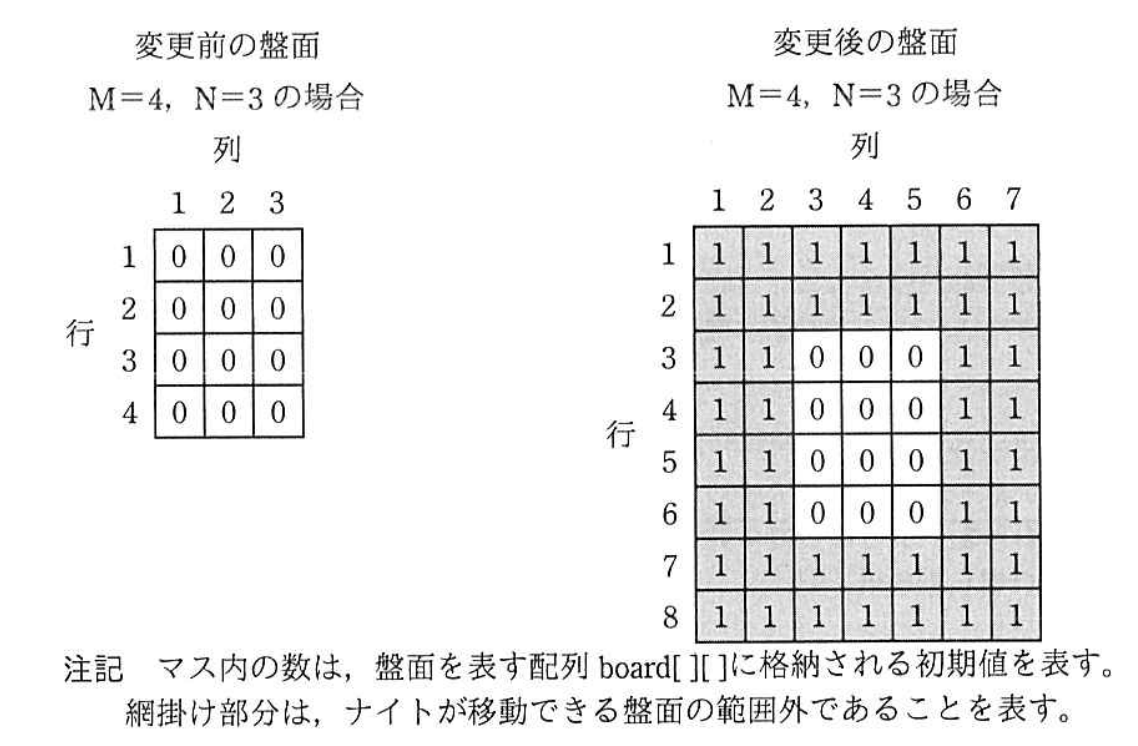
ナイトの巡歴問題とは，M 行 N 列（以下，M×N マスという）の盤面上でチェスの駒の一種であるナイトを移動させ，全てのマスを 1 回ずつ通過する経路を発見する問題である。

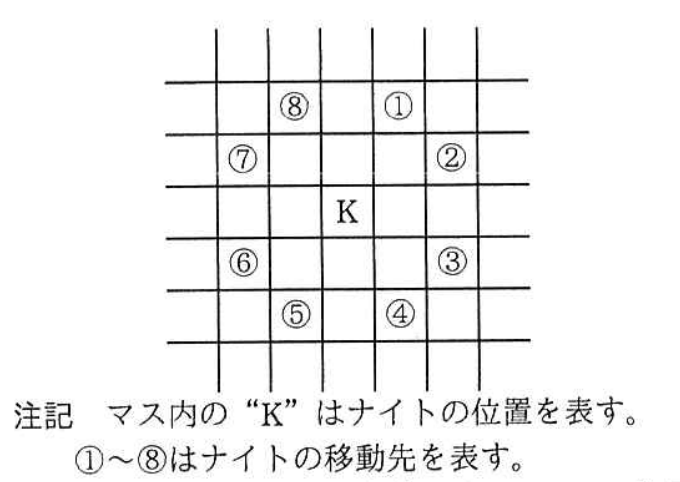
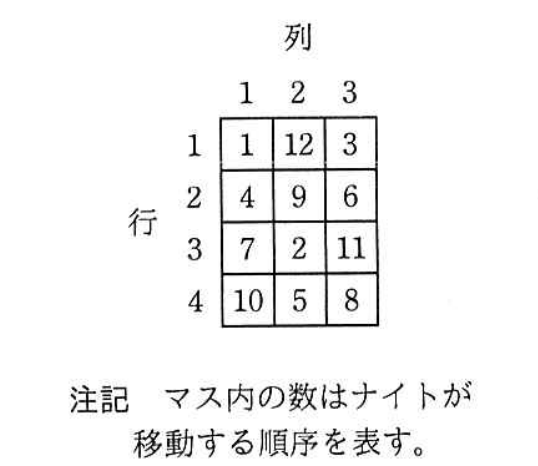
ナイト（K）が 1 回で移動できるマス（以下，移動先という）の位置を図 1 に示す。また，4×3 マスの場合のナイトの巡歴問題の解の一つを図 2 に示す。図 2 に示す，ナイトの移動する順序を表す数を，移動順序という。

なお，行番号は上から下，列番号は左から右に増加する。

M×N マスのナイトの巡歴問題について，行 1 列 1 のマスを起点とする全ての経路を求める処理の概要を示す。この処理は，再帰による深さ優先探索として実現されている。

【ナイトの巡歴問題の処理の概要】

(1) 移動順序 1，行 1，列 1 で，再帰関数 search を呼び出す。

再帰関数 search（移動順序，行，列）

(i) 行と列で指定されるマス（以下，現在のマスという）が盤面の範囲外，又は既に通過したマスであった場合，何もせずに再帰関数 search の呼出し元へ戻る。

(ii) (i)以外の場合，現在のマスに，移動順序を記録する。

(ii-1) 記録した移動順序が M×N に等しい場合，その経路を解の一つとして出力する。

(ii-2) (ii-1)以外の場合，現在のマスを起点とした図 1 の移動先①～⑧のそれぞれについて再帰関数 search を呼び出す。引数の行と列には，移動先を指定する。移動順序には，現在の移動順序に 1 を加えたものを指定する。

(ii-3) 現在のマスの移動順序を取り消して，マスを通過していない状態に戻す。

(ii-4) 再帰関数 search の呼出し元へ戻る。

(2) 終了する。

この処理の概要をプログラムに実装するために，M×N マスの盤面，ナイトの移動先をそれぞれ次のデータ構造で表現することにした。

・M×N マスの盤面を 2 次元配列 board[M][N] で表現する。添字は 1 から始まる。各要素の初期値は 0 とし，ナイトが通過した場合に，移動順序を各要素に格納する。

・ナイトの各移動先について，行方向，列方向，それぞれの移動量を dv[ ]，dh[ ] の配列で表現する。添字は 1 から始まる。dv[ ]，dh[ ] はそれぞれ，八つの要素をもち，図 1 の移動先①～⑧に対応する行方向，列方向の移動量を設定する。

dv[ ]，dh[ ] に設定する値を表 1 に示す。①の場合，行方向は上に 2 マス，列方向は右に 1 マス移動するので，dv[1] は -2，dh[1] は 1 となる。

【ナイトの巡歴問題の解法のプログラム】

M×N マスのナイトの巡歴問題について，解法のプログラムを考える。

解法のプログラムで使用する定数，変数及び関数を表 2 に示す。

再帰関数 search のプログラムを図 3 に，解答を印字する関数 printBoard のプログラムを図 4 に，メインプログラムを図 5 に示す。

なお，左側の番号はプログラムの行番号を示す。

1: function search( i, v, h )
2:   if( v が 1 以上，かつ，m 以下 )
3:     if( h が 1 以上，かつ，n 以下 )
4:       if( board[v][h] が 0 )
5:         board[v][h] ← i
6:         if( ウ )
7:           printBoard()
8:           printFlag ← 1
9:         else
10:          for( j を 1 から 8 まで 1 ずつ増やす)
11:            search( エ, オ, カ )
12:          endfor
13:        endif
14:        キ
15:      endif
16:    endif
17:  endif
18: endfunction

19: function printBoard()
20:   for( v を 1 から m まで 1 ずつ増やす )
21:     for( h を 1 から n まで 1 ずつ増やす )
22:       print( board[v][h] )
23:     endfor
24:     print( 改行 )
25:   endfor
26: endfunction

27: function main()
28:   m ← M
29:   n ← N
30:   board[][] を初期化する
31:   printFlag ← 0
32:   search( 1, 1, 1 )
33:   if( printFlag が 0 )
34:     print( "解答がありません" )
35:   endif
36: endfunction

【盤面の表現の変更】

ナイトの移動先が盤面の範囲外となった場合の判定処理を簡略化するために，図 6 のように盤面をナイトが移動できるマスが全て含まれる範囲まで拡大して表現する。

この変更に合わせて①関数 printBoard の変更，②メインプログラムの変更，③再帰関数 search の一部の行の削除を同時に行うことによって，プログラムを短縮することができる。

<p>変更後の盤面 M=4，N=3の場合</p>
<table>
  <tr><td></td><td>列</td><td></td><td></td><td></td><td></td><td></td><td></td></tr>
  <tr><td></td><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td><td>6</td><td>7</td></tr>
  <tr><td>行</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>0</td><td>0</td><td>0</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>0</td><td>0</td><td>0</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>0</td><td>0</td><td>0</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>0</td><td>0</td><td>0</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td></tr>
  <tr><td></td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td><td>1</td></tr>
</table>