応用情報技術者試験 過去問 2023年(令和5年) 秋期 午後 問3
2分探索木
2分探索木とは、木に含まれる全てのノードがキー値をもち、各ノードNが次の二つの条件を満たす2分木のことである。ここで、重複したキー値をもつノードは存在しないものとする。
- Nの左側の部分木にある全てのノードのキー値は、Nのキー値よりも小さい。
- Nの右側の部分木にある全てのノードのキー値は、Nのキー値よりも大きい。
2分探索木の例を図1に示す。図中の数字はキー値を表している。
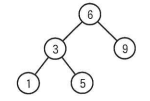
2分探索木をプログラムで表現するために、ノードを表す構造体Nodeを定義する。構造体Nodeの構成要素を表1に示す。
| 構成要素 | 説明 |
|---|---|
| key | キー値 |
| left | 左側の子ノードへの参照 |
| right | 右側の子ノードへの参照 |
構造体Nodeを新しく生成し、その構造体への参照を変数pに代入する式を次のように書く。
p ← new Node(k)
ここで、引数kは生成するノードのキー値であり、構成要素keyの初期値となる。構成要素leftおよびrightは、参照するノードがないこと(以下、空のノードという)を表すNULLで初期化される。また、生成したpの各構成要素へのアクセスには"."を用いる。例えば、キー値はp.keyでアクセスする。
2分探索木におけるノードの探索・挿入
キー値kをもつノードの探索は次の手順で行う。
- 探索対象の2分探索木の根を参照する変数をtとする。
- tが空のノードであるかを調べる。
- tが空のノードであれば、探索失敗と判断して探索を終了する。
- tが空のノードでなければ、tのキー値t.keyとkを比較する。
- t.key = kの場合、探索成功と判断して探索を終了する。
- t.key > kの場合、tの左側の子ノードを新たなtとして(2)から処理を行う。
- t.key < kの場合、tの右側の子ノードを新たなtとして(2)から処理を行う。
キー値kをもつノードKの挿入は、探索と同様の手順で根から順にたどっていき、空のノードが見つかった位置にノードKを追加することで行う。ただし、キー値kと同じキー値をもつノードが既に2分探索木中に存在するときは何もしない。
これらの手順によって探索を行う関数searchのプログラムを図2に、挿入を行う関数insertのプログラムを図3に示す。関数searchは、探索に成功した場合は見つかったノードへの参照を返し、失敗した場合はNULLを返す。関数insertは、得られた木の根への参照を返す。
// tが参照するノードを根とする木から
// キー値がkであるノードを探索する
function search(t, k)
if(t が NULL と等しい)
return NULL
elseif(t.key が k と等しい)
return t
elseif(t.key が k より大きい)
return search(t.left, k)
else // t.key が k より小さい場合
return search(t.right, k)
endif
endfunction
// tが参照するノードを根とする木に
// キー値がkであるノードを挿入する
function insert(t, k)
if(t が NULL と等しい)
t ← new Node(k)
elseif(t.key が k より大きい)
t.left ← insert(t.left, k)
elseif(t.key が k より小さい)
t.right ← insert(t.right, k)
endif
return t
endfunction
関数searchを用いてノードの総数がn個の2分探索木を探索するとき、探索に掛かる最悪の場合の時間計算量(以下、最悪時間計算量という)はO(ア)である。これは葉を除く全てのノードについて左右のどちらかにだけ子ノードが存在する場合である。一方で、葉を除く全てのノードに左右両方の子ノードが存在し、また、全ての葉の深さが等しい完全な2分探索木であれば、最悪時間計算量はO(イ)となる。したがって、高速に探索するためには、なるべく左右両方の子ノードが存在するように配置して、高さができるだけ低くなるように構成した木であることが望ましい。このような木のことを平衡2分探索木という。
2分探索木における回転操作
2分探索木中のノードXとXの左側の子ノードYについて、XをYの右側の子に、元のYの右側の部分木をXの左側の部分木にする変形操作を右回転という。逆の操作を左回転という。回転操作後も2分探索木の条件は維持される。木の回転の様子を図4に示す。ここで、t₁〜t₃は部分木を表している。また、根からt₁〜t₃の最も深いノードまでの深さを、図4(a)ではd₁〜d₃、図4(b)ではd₁'〜d₃'でそれぞれ表している。ここで、d₁' = d₁ - 1、d₂' = d₂、d₃' = d₃ + 1、が成り立つ。
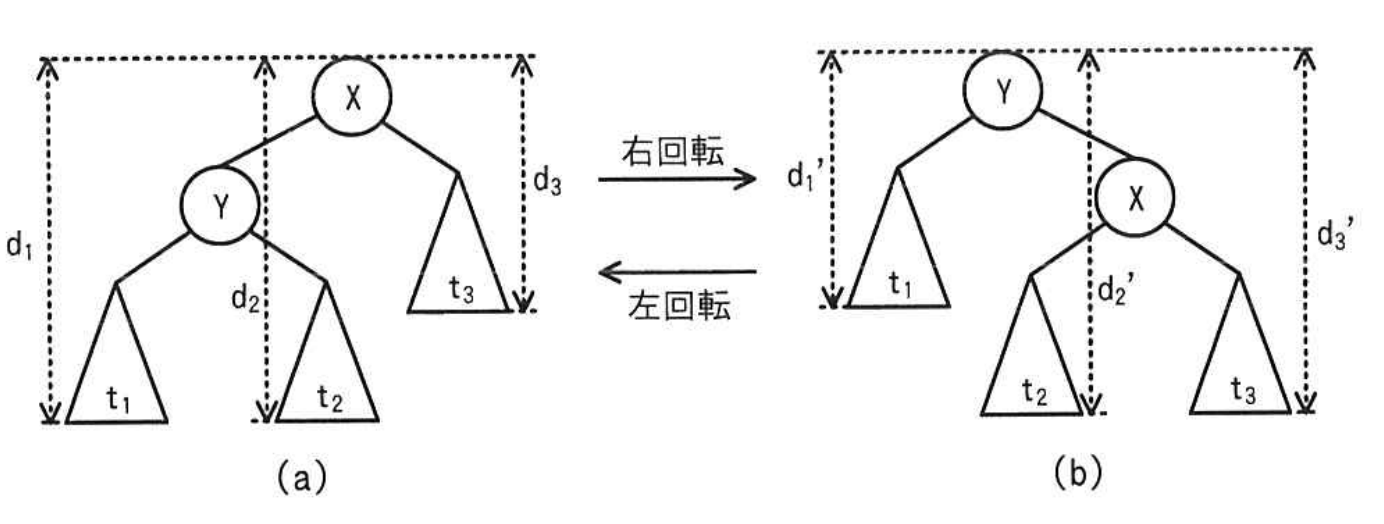
右回転を行う関数rotateRのプログラムを図5に、左回転を行う関数rotateLのプログラムを図6に示す。これらの関数は、回転した結果として得られた木の根への参照を返す。
// tが参照するノードを根とする木に対して
// 右回転を行う
function rotateR(t)
a ← t.left
b ← a.right
a.right ← t
t.left ← b
return a
endfunction
// tが参照するノードを根とする木に対して
// 左回転を行う
function rotateL(t)
a ← t.right
b ← a.left
a.left ← t
t.right ← b
return a
endfunction
回転操作を利用した平衡2分探索木の構成
全てのノードについて左右の部分木の高さの差が1以下という条件(以下、条件Balという)を考える。条件Balを満たす場合、完全ではないとしても比較的左右均等にノードが配置された木になる。
条件Balを満たす2分探索木Wに対して図3の関数insertを用いてノードを挿入した2分探索木をW'とすると、ノードが挿入される位置によっては左右の部分木の高さの差が2になるノードが生じるので、W'は条件Balを満たさなくなることがある。その場合、挿入したノードから根まで、親をたどった各ノードTに対して順に次の手順を適用することで、条件Balを満たすようにW'を変形することができる。
- Tの左側の部分木の高さがTの右側の部分木の高さより2大きい場合
Tを根とする部分木に対して右回転を行う。ただし、Tの左側の子ノードUについて、Uの右側の部分木の方がUの左側の部分木よりも高い場合は、先にUを根とする部分木に対して左回転を行う。
- Tの右側の部分木の高さがTの左側の部分木の高さより2大きい場合
Tを根とする部分木に対して左回転を行う。ただし、Tの右側の子ノードVについて、Vの左側の部分木の方がVの右側の部分木よりも高い場合は、先にVを根とする部分木に対して右回転を行う。
この手順(1)、(2)によって木を変形する関数balanceのプログラムを図7に、関数balanceを適用するように関数insertを修正した関数insertBのプログラムを図8に示す。ここで、関数heightは、引数で与えられたノードを根とする木の高さを返す関数である。関数balanceは、変形の結果として得られた木の根への参照を返す。
// tが参照するノードを根とする木を
// 条件Balを満たすように変形する
function balance(t)
h1 ← height(t.left) - height(t.right)
if(ウ)
h2 ← エ
if(h2 が 0 より大きい)
t.left ← rotateL(t.left)
endif
t ← rotateR(t)
elseif(オ)
h3 ← カ
if(h3 が 0 より大きい)
t.right ← rotateR(t.right)
endif
t ← rotateL(t)
endif
return t
endfunction
// tが参照するノードを根とする木に
// キー値がkであるノードを挿入する
function insertB(t, k)
if(t が NULL と等しい)
t ← new Node(k)
elseif(t.key が k より大きい)
t.left ← insertB(t.left, k)
elseif(t.key が k より小さい)
t.right ← insertB(t.right, k)
endif
t ← balance(t) // 追加
return t
endfunction
条件Balを満たすノードの総数がn個の2分探索木に対して関数insertBを実行した場合、挿入に掛かる最悪時間計算量はO(キ)となる。