応用情報技術者試験 過去問 2018年(平成30年) 秋期 午後 問3
ウェーブレット木
ウェーブレット木は、文字列内の文字の出現頻度を集計する場合などに用いられる2分木である。ウェーブレット木は、文字列内に含まれる文字を符号化して、それを基に構築される。特に計算に必要な作業領域を小さくできるので、文字列が長大な場合に効果的である。
例えば、DNA は A(アデニン)、C(シトシン)、G(グアニン)、T(チミン)の 4種類の文字の配列で表すことができ、その配列は長大になることが多いので、ウェーブレット木は DNA の塩基配列(以下,DNA 配列という)の構造解析に適している。
ウェーブレット木において、文字の出現回数を数える操作と文字の出現位置を返す操作を組み合わせることによって、文字列の様々な操作を実現することができる。本問では、文字の出現回数を数える操作を扱う。
ウェーブレット木の構築
文字の種類の個数が 4 の場合を考える。DNA 配列を例に文字列 P を"CTCGAGAGTA" とするとき、ウェーブレット木が構築される様子を図1に示す。
ここで、2分木の頂点のノードを根と呼び、子をもたないノードを葉と呼ぶ。根からノードまでの経路の長さ(経路に含まれるノードの個数−1)を、そのノードの深さと呼ぶ。各ノードにはキー値を登録する。
図1では、文字列 P の文字 A を 00、文字 C を 01、文字 G を 10、文字 T を 11 の 2ビットのビット列に符号化して、ウェーブレット木を構築する様子を示している。また、図 1 の文字列の振り分けは、ウェーブレット木によって文字列 P が振り分けられる様子を示している。
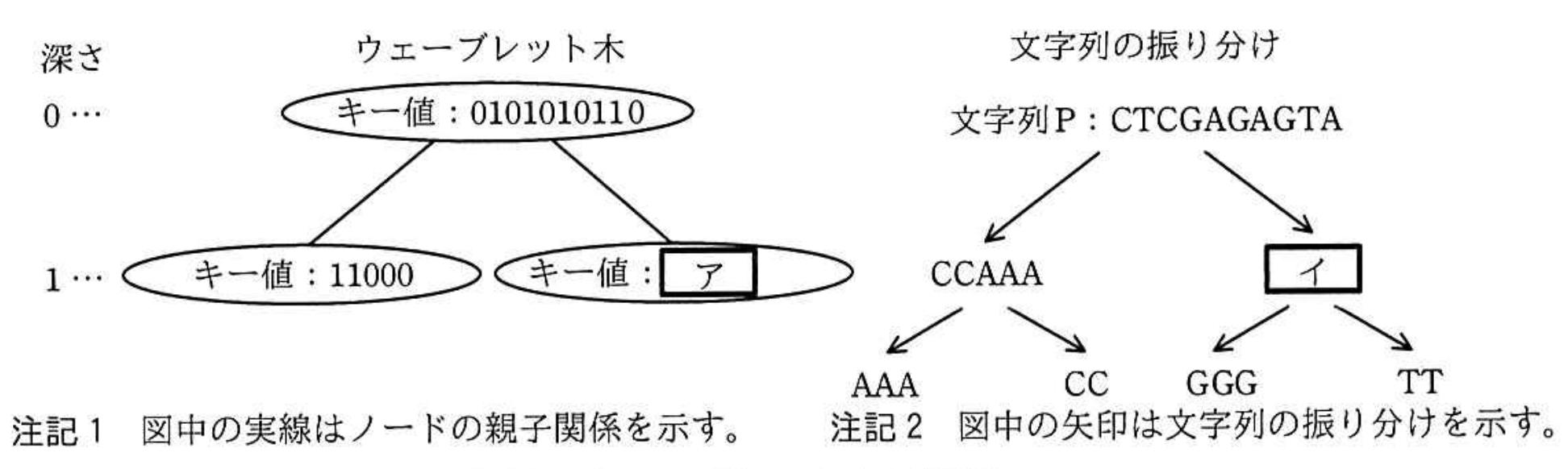
ウェーブレット木は、次の(1)~(3)の手順で構築する。
- 根(深さ 0)を生成し、文字列 P を対応付ける。
- ノードに対応する文字列の各文字を表す符号に対して、ノードの深さに応じて決まるビット位置のビットの値を取り出し、文字の並びと同じ順番で並べてビット列として構成したものをキー値としてノードに登録する。ここで、ノードの深さに応じて決まるビット位置は、"左から(深さ+1)番目"とする。
ノードが根の場合は、ビット位置は左から(0+1=1)番目となるので、図 2 に示すように、文字列 P "CTCGAGAGTA" に対応する根のキー値はビット列 0101010110 となる。
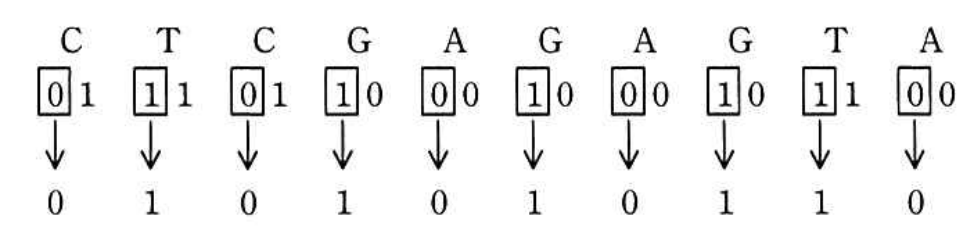
図2 根のキー値 - キー値のビット列を左から 1 ビットずつ順番に見ていき、キー値の元になった文字列から、そのビットに対応する文字を、ビットの値が 0 の場合とビットの値が 1 の場合とで分けて取り出し、それぞれの文字を順番に並べて新たな文字列を作成する。
文字列 P に対応する根のキー値の場合は、ビットの値が 0 の場合の文字列として "CCAAA" を取り出し、ビットの値が 1 の場合の文字列として "イ" を取り出す。
ビットの値が 0 の場合に取り出した文字列内の文字が 2 種類以上の場合は、その文字列に対応する新たなノードを生成して、左の子ノードとする。取り出した文字列内の文字が 1 種類の場合は、新たなノードは生成しない。
ビットの値が 1 の場合に取り出した文字列内の文字が 2 種類以上の場合は、その文字列に対応する新たなノードを生成して、右の子ノードとする。取り出した文字列内の文字が 1 種類の場合は、新たなノードは生成しない。
生成した子ノードに対して、(2),(3)の処理を繰り返す。新たなノードが生成されなかった場合は、処理を終了する。
文字の出現回数を数える操作
文字列 P 全体での文字 C(=01)の出現回数は、次の(1),(2)の手順で求める。
- 文字 C の符号の左から 1 番目のビットの値は 0 なので、文字 C は根から左の子ノードに振り分けられる。左の子ノードに振り分けられる文字の個数は、根のキー値の 0 の個数に等しく、ウである。
- 文字 C の符号の左から 2 番目のビットの値は 1 である。(1)で振り分けられた左の子ノードのキー値の 1 の個数は 2 で、このノードは葉であるので、これが文字列 P 全体での文字 C の出現回数となる。
文字の出現回数を数えるプログラム
与えられた文字列 Q 内に含まれる文字の種類の個数を σ とするとき、あらかじめ生成したウェーブレット木を用いて、与えられた文字列内で指定した文字の出現回数を数えるプログラムを考える。ウェーブレット木の各ノードを表す構造体 Node を表1に示す。左の子ノード、又は右の子ノードがない場合は、それぞれ、left, right には NULL を格納する。
| 構成要素 | 説明 |
|---|---|
| key | ノードのキー値をビット列として格納 |
| left | 左の子ノードへのポインタを格納 |
| right | 右の子ノードへのポインタを格納 |
文字列 Q に対応して生成したウェーブレット木の根へのポインタを root とする。
文字列 Q 内に存在する一つの文字(以下,対象文字という)をビット列に符号化して、整数(0~σ-1)に変換したものを r とする。
このとき、文字列 Q の 1 文字目から m 文字目までの部分文字列で、対象文字の出現回数を数える関数 rank(root, m, r) のプログラムを図 3 に示す。
文字の符号化に必要な最小のビット数は、大域変数 DEPTH に格納されているものとする。
function rank(root,m,r)
nodep ← root
d ← 1 // 符号中の左からのビット位置の初期化
n ← m // 検索対象の文字列の長さの初期化
while( nodep が NULL でない )
count ← 0
// r に対応するビット列の左から d 番目のビット位置のビットの値を b に格納
x ← ( 1 を左に エ ビットシフトした値 )
x ← ( x and オ ) // and はビットごとの論理積
b ← ( x を右に エ ビットシフトした値 ) // b は 0 か 1 の値
for ( i を 1 から n まで 1 ずつ増やす)
if ( b が nodep.key の左から i 番目のビット位置のビットの値と等しい)
count ← count + 1
endif
endfor
if ( b が カ と等しい )
nodep ← nodep.left
else
nodep ← nodep.right
endif
n ← キ
d ← d + 1
end while
return n
end function
ウェーブレット木の評価
文字列 Q が与えられたとき、文字列 Q の長さを N、文字の種類の個数を σ とする。ここで、議論を簡潔にするために σ は 2 以上の 2 のべき乗とする。
文字列 Q が与えられたときのウェーブレット木の構築時間は、文字ごとに log₂(ク)個所のノードで操作を行い、各ノードでの操作は定数時間で行うことができるので、合計で O(ケ × log₂(ク))である。
構築されたウェーブレット木が保持するキー値のビット列の長さの総和は、コである。