応用情報技術者試験 過去問 2023年(令和5年) 春期 午後 問3
多倍長整数の演算
コンピュータが一度に処理できる整数の最大桁には、CPUが一度に扱える情報量に依存した限界がある。一度に扱える桁数を超える演算を行う一つの方法として、10を基数とした多倍長整数(以下、多倍長整数という)を用いる方法がある。
多倍長整数の加減算
多倍長整数の演算では、整数の桁ごとの値を、1の位から順に1次元配列に格納して管理する。例えば整数123は、要素数が3の配列に(3,2,1)を格納して表現する。
多倍長整数の加算は、"桁ごとの加算"の後、"繰り上がり"を処理することで行う。
456+789を計算した例を図1に示す。

"桁ごとの加算"を行うと、配列の内容は{15,13,11}となる。1の位は15になるが、15は10×1+5なので、10の位である13に1を繰り上げて{5,14,11}とする。
これを最上位まで繰り返す。最上位で繰り上がりが発生する場合は、配列の要素数を増やして対応する。減算も同様に"桁ごとの減算"と"繰り下がり"との処理で計算できる。
多倍長整数の乗算
多倍長整数の乗算については、計算量を削減するアルゴリズムが考案されており、その中の一つにカラツバ法がある。ここでは、桁数が2のべき乗で、同じ桁数をもった正の整数同士の乗算について、カラツバ法を適用した計算を行うことを考える。桁数が2のべき乗でない整数や、桁数が異なる整数同士の乗算を扱う場合は、上位の桁を0で埋めて処理する。例えば、123×4は0123×0004として扱う。
ツリー構造の構築
カラツバ法を適用した乗算のアルゴリズムは、計算のためのツリー構造(以下、ツリーという)を作る処理と、ツリーを用いて演算をする処理から成る。ツリーは、多倍長整数の乗算の式を一つのノードとし、一つのノードは3個の子ノードをもつ。
M桁×M桁の乗算の式について、乗算記号の左右にある値を、それぞれM/2桁ずつに分けてA,B,C,Dの四つの多倍長整数を作る。これらの整数を使って、①A×C,②B×D,③(A+B)×(C+D)の3個の子ノードを作り、M/2桁×M/2桁の乗算を行う層を作る。(A+B),(C+D)は多倍長整数の加算の結果であるが、ここでは"桁ごとの加算"だけの処理を行い、"繰り上がり"の処理はツリーを用いて行う演算の最後でまとめて行う。生成した子ノードについても同じ手順を繰り返し、1桁×1桁の乗算を行う最下層のノードまで展開する。
1234×5678についてのツリーを図2に示す。図2の層2の場合、①は12×56,②は34×78,③は46×134となる。③の(C+D)は、"桁ごとの加算"だけの処理を行うと、10の位が5+7=12,1の位が6+8=14となるので、12×10+14=134となる。
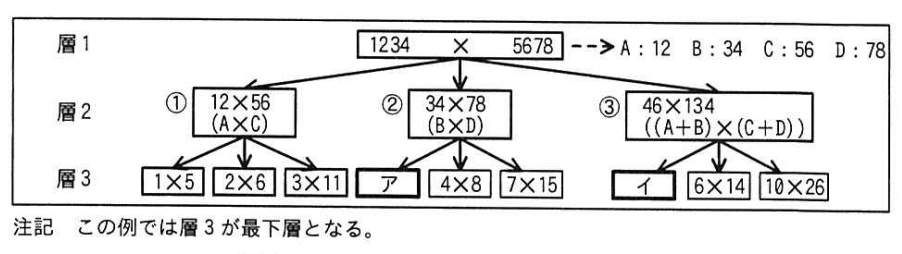
ツリーを用いた演算
ツリーの最下層のノードは、整数の乗算だけで計算できる。最下層以外の層は、子ノードの計算結果を使って、次の式で計算できることが分かっている。ここで、α,β,γは、それぞれ子ノード①,②,③の乗算の計算結果を、Kは対象のノードの桁数を表す。
α×10^K + (γ - α - β)×10^(K/2) + β ……(1)
図2のルートノードの場合、K=4,α=672,β=2652,γ=6164なので、計算結果は次のとおりとなる。
672×10000+(6164-672-2652)×100+2652=7006652
多倍長整数の乗算のプログラム
桁数が2のべき乗の多倍長整数val1,val2の乗算を行うプログラムを作成した。
プログラム中で利用する多倍長整数と、ツリーのノードは構造体で取り扱う。構造体の型と要素を表1に示す。構造体の各要素には、構造体の変数名,要素名でアクセスできる。また、配列の添字は1から始まる。
| 構造体の型 | 要素名 | 要素の型 | 内容 |
|---|---|---|---|
| 多倍長整数 | N | 整数 | 多倍長整数の桁数 |
| values | 整数の配列 | 桁ごとの値を管理する1次元配列。1の位の値から順に値を格納する。配列の要素は、必要な桁を全て格納するのに十分な数が確保されているものとする。 | |
| ノード | N | 整数 | ノードが取り扱う多倍長整数の桁数。図2の1234×5678のノードの場合は4である。 |
| val1 | 多倍長整数 | 乗算記号の左側の値 | |
| val2 | 多倍長整数 | 乗算記号の右側の値 | |
| result | 多倍長整数 | 乗算の計算結果 |
多倍長整数の操作を行う関数を表2に、プログラムで使用する主な変数,配列及び関数を表3に,与えられた二つの多倍長整数からツリーを構築するプログラムを図3に,そのツリーを用いて演算を行うプログラムを図4に,それぞれ示す。表2,表3中のp,q,v1,v2の型は多倍長整数である。また,図3,図4中の変数は全て大域変数である。
| 名称 | 型 | 内容 |
|---|---|---|
| add(p, q) | 多倍長整数 | pとqについて、"桁ごとの加算"を行う。 |
| carry(p) | 多倍長整数 | pについて"繰り上がり","繰り下がり"の処理を行う。 |
| left(p, k) | 多倍長整数 | pについて、valuesの添字が大きい方のk個の要素を返す。pのvaluesが{4, 3, 2, 1}、kが2であれば、valuesが{2, 1}の多倍長整数を返す。 |
| right(p, k) | 多倍長整数 | pについて、valuesの添字が小さい方のk個の要素を返す。pのvaluesが{4, 3, 2, 1}、kが2であれば、valuesが{4, 3}の多倍長整数を返す。 |
| tradd(p, k) | 多倍長整数 | add(left(p, k), right(p, k))の結果を返す。 |
| shift(p, k) | 多倍長整数 | pを10^k倍する。 |
| sub(p, q) | 多倍長整数 | pとqについて、"桁ごとの減算"を行いp-qを返す。 |
| 名称 | 種類 | 型 | 内容 |
|---|---|---|---|
| elements[] | 配列 | ノード | ツリーのノードを管理する配列。ルートノードを先頭に、各層の左側のノードから順に要素を格納する。図2の場合は、{1234×5678, 12×56, 34×78, 46×134, 1×5, 2×6, ...}の順に格納する。 |
| layer_top[] | 配列 | 整数 | ルートノードから順に、各層の左端のノードの、elements配列上での添字を格納する。図2の場合は1234×5678, 12×56, 1×5の添字に対応する{1, 2, 5}が入る。 |
| mod(m, k) | 関数 | 整数 | mをkで割った剰余を整数で返す。 |
| new_elem(k,v1,v2) | 関数 | ノード | 取り扱う多倍長整数の桁数がkで、v1×v2の乗算を表すノード構造体を新規に一つ作成して返す。 |
| pow(m, k) | 関数 | 整数 | mのk乗を整数で返す。kが0の場合は1を返す。 |
| t_depth | 変数 | 整数 | ツリーの層数。図2の場合は3である。 |
| val1, val2 | 変数 | 多倍長整数 | 乗算する対象の二つの値。図2の場合、ルートノードの二つの値で、val1は1234, val2は5678である。 |
| answer | 変数 | 多倍長整数 | 乗算の計算結果を格納する変数 |
// ツリーの各層の、elements配列上での先頭インデックスを算出する
layer_top[1] ← 1 // ルートノードは先頭なので1を入れる
for (iを1からt_depth − 1まで1ずつ増やす)
layer_top[i + 1] ← layer_top[i] + ウ
endfor
// ツリーを構築する
elements[1] ← new_elem(val1.N, val1, val2) // ルートノードを用意。桁数はval1の桁数を使う
for (dpを1からt_depth − 1まで1ずつ増やす) // ルートノードの層から、最下層以外の層を順に処理
for (iを1からpow(3, dp − 1)まで1ずつ増やす) // 親ノードになる層の要素数だけ繰り返す
pe ← elements[layer_top[dp] + (i − 1)] // 親ノードを取得
cn ← pe.N / 2 // 子ノードの桁数を算出
tidx ← layer_top[dp + 1] + エ // 子ノード①へのインデックス
elements[tidx ] ← new_elem(cn, left(オ, cn), left(カ, cn))
elements[tidx + 1] ← new_elem(cn, right(オ, cn), right(カ, cn))
elements[tidx + 2] ← new_elem(cn, tradd(オ, cn), tradd(カ, cn))
endfor
endfor
// 最下層の計算
for (iを1からpow(3, t_depth − 1)まで1ずつ増やす) // 最下層の要素数は3^(t_depth-1)個
el ← elements[layer_top[t_depth] + (i − 1)] // 最下層のノード
mul ← el.val1.values[1] * el.val2.values[1] // 最下層の乗算
el.result.N ← 2 // 計算結果は2桁の多倍長整数
el.result.values[1] ← キ // 1の位
el.result.values[2] ← mul / 10 // 10の位
endfor
// 最下層以外の計算
for (dpをt_depth − 1から1まで1ずつ減らす) // 最下層より一つ上の層から順に処理
for (iを1からpow(3, dp − 1)まで1ずつ増やす) // 各層の要素数だけ繰り返す
el ← elements[layer_top[dp] + (i − 1)] // 計算対象のノード
cidx ← layer_top[dp + 1] + ク // 子ノード①へのインデックス
s1 ← sub(ケ, elements[cidx].result) // γ − α を計算
s2 ← sub(s1, elements[cidx + 1].result) // γ − α − β を計算
p1 ← shift(elements[cidx].result, el.N) // α × 10^K を計算
p2 ← shift(s2, el.N / 2) // (γ − α − β) × 10^(K/2) を計算
p3 ← elements[cidx + 1].result // β を取得
el.result ← add(add(p1, p2), p3)
endfor
endfor
// 繰り上がり処理
answer ← carry(elements[1].result) // 計算結果をanswerに格納